Примеры решений уравнений с косинусом: от простого к сложному

На этой странице вы найдете подробные примеры решений уравнений вида cos(x)=a, а также полезные советы и методы для их решения.

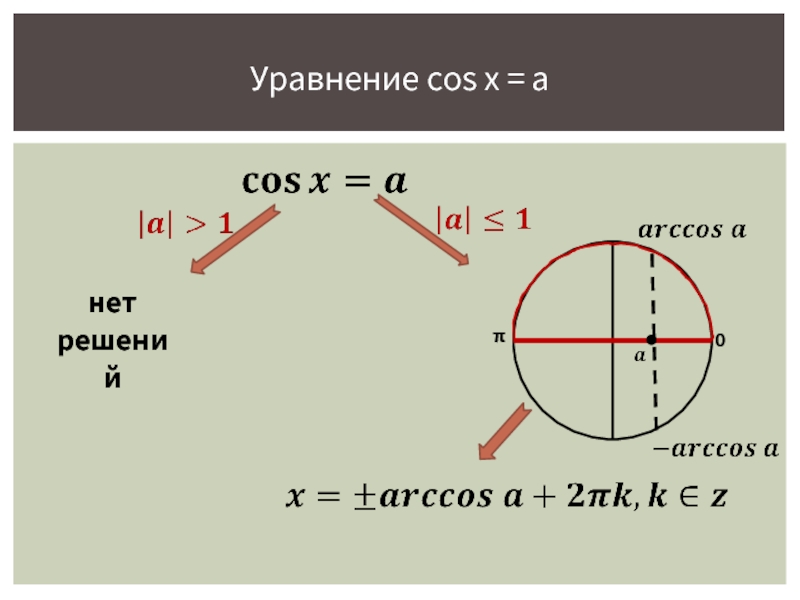
Определите допустимые значения для параметра a. Для уравнения cos(x)=a параметр a должен находиться в диапазоне от -1 до 1.

Преобразуйте уравнение к стандартному виду. Если уравнение имеет вид cos(x)=a, проверьте, можно ли его упростить или преобразовать.

Рассмотрите периодичность функции косинуса. Помните, что cos(x) имеет период 2π, и используйте это для поиска всех решений.

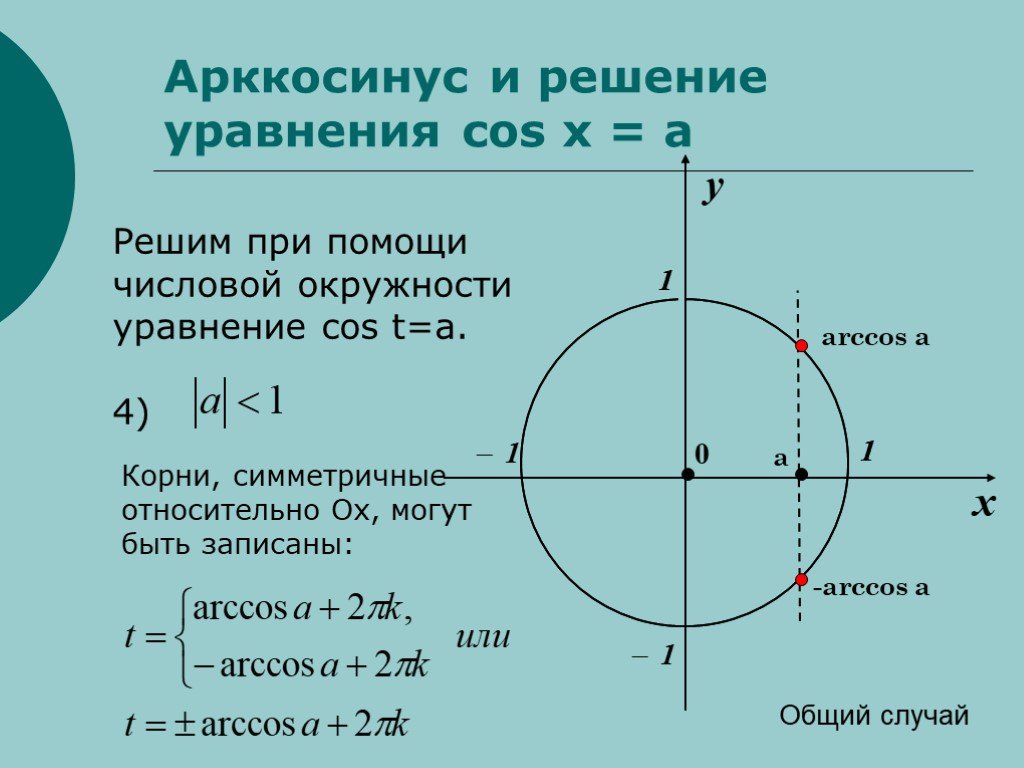
Используйте основное решение. Основное решение уравнения cos(x)=a находится как arccos(a) + 2πk и -arccos(a) + 2πk, где k - целое число.

Проверьте найденные решения. Всегда подставляйте найденные значения x обратно в исходное уравнение, чтобы убедиться в их правильности.

Используйте графический метод. Постройте график функции cos(x) и горизонтальную линию y=a, чтобы визуально определить точки пересечения.

Рассмотрите симметрию функции косинуса. Используйте симметрические свойства косинуса для упрощения поиска решений.

При необходимости используйте численные методы. Если уравнение не поддается аналитическому решению, используйте численные методы, такие как метод бисекции или метод Ньютона.

Используйте калькуляторы и программы. Специализированные математические калькуляторы и программы могут помочь быстро найти решения.

Практикуйтесь на различных примерах. Чем больше примеров вы решите, тем лучше будете понимать методы решения уравнений вида cos(x)=a.