Основные принципы весовой матрицы графа в информатике

Весовая матрица графа является важным инструментом в информатике, позволяющим эффективно представлять и анализировать взвешенные графы. Этот инструмент находит широкое применение в алгоритмах и задачах, связанных с теорией графов, и помогает в решении множества вычислительных задач.

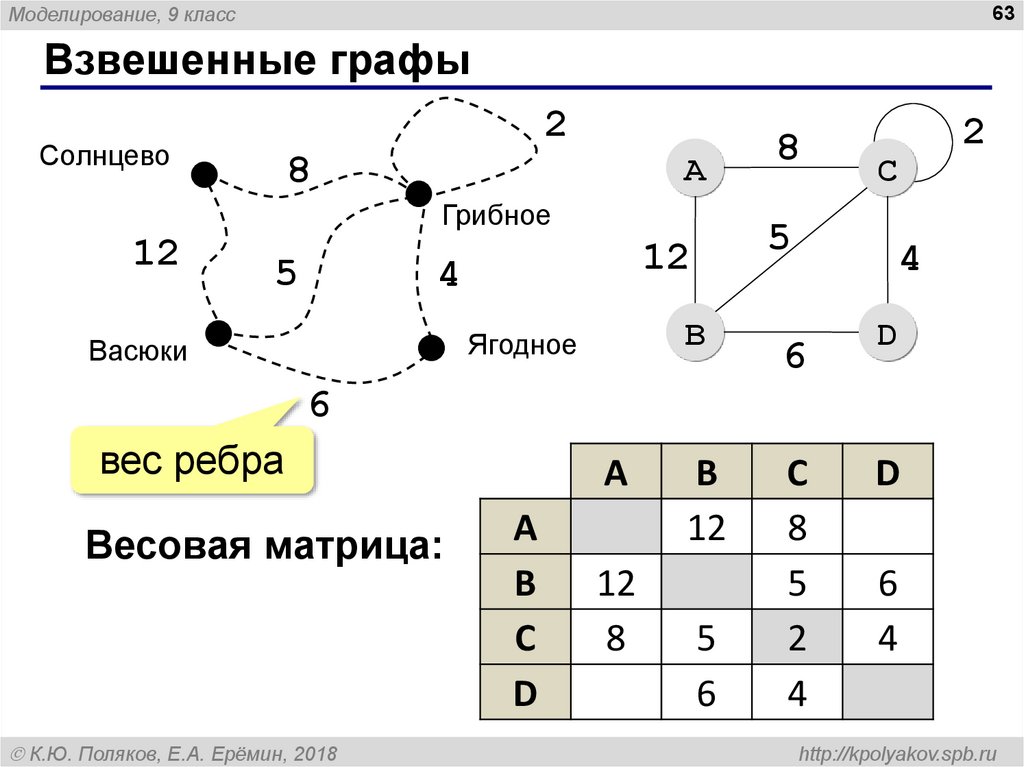
Для создания весовой матрицы графа начните с определения всех вершин графа и установите веса ребер между ними.

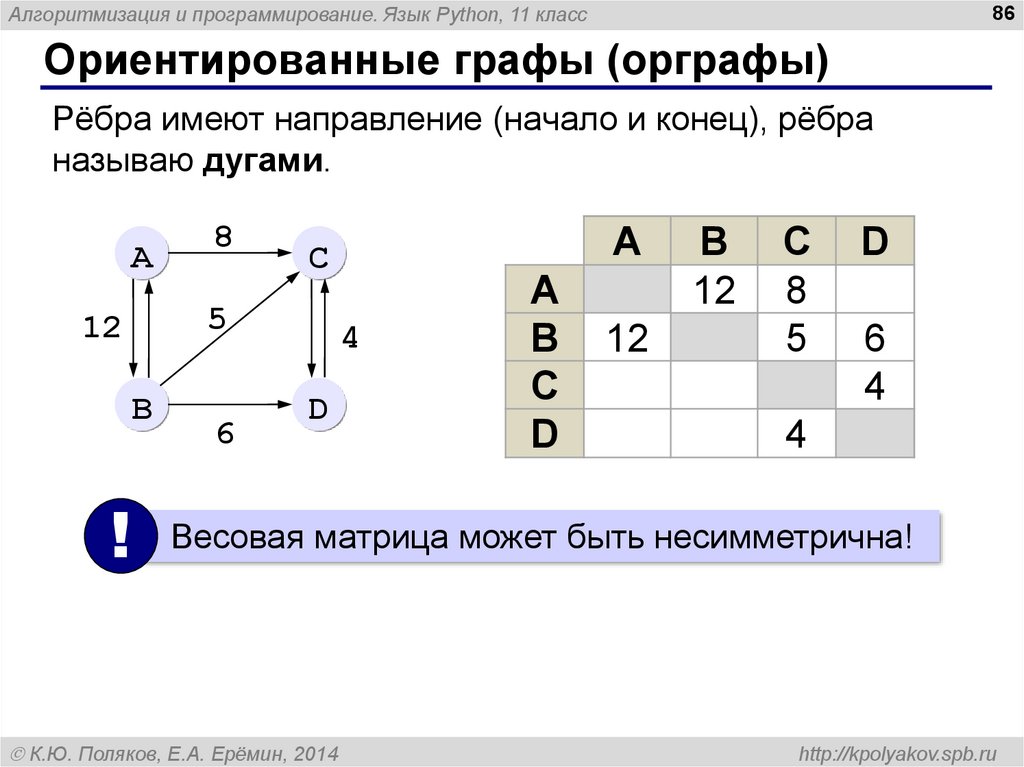
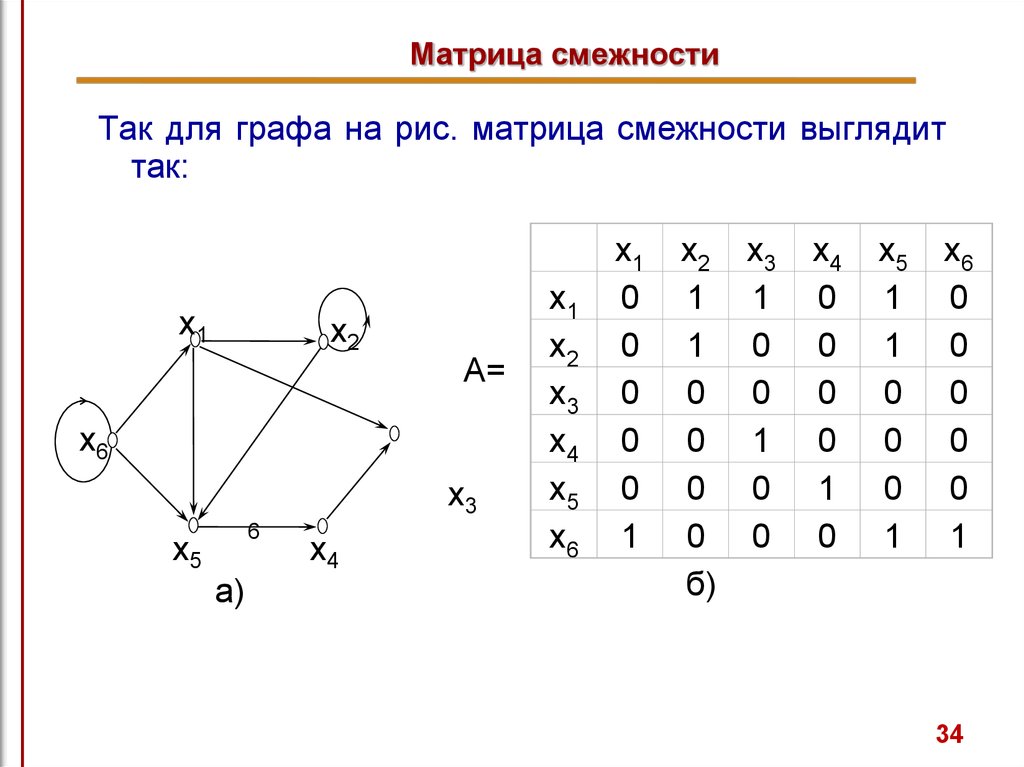
Используйте двумерный массив или матрицу для представления весовой матрицы, где строки и столбцы соответствуют вершинам графа.

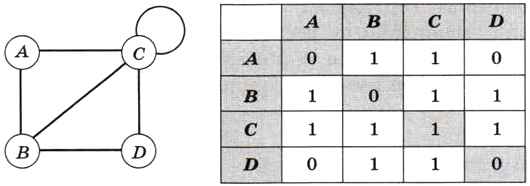
Помните, что если между двумя вершинами нет ребра, то соответствующий элемент матрицы должен быть равен бесконечности или нулю, в зависимости от используемой конвенции.

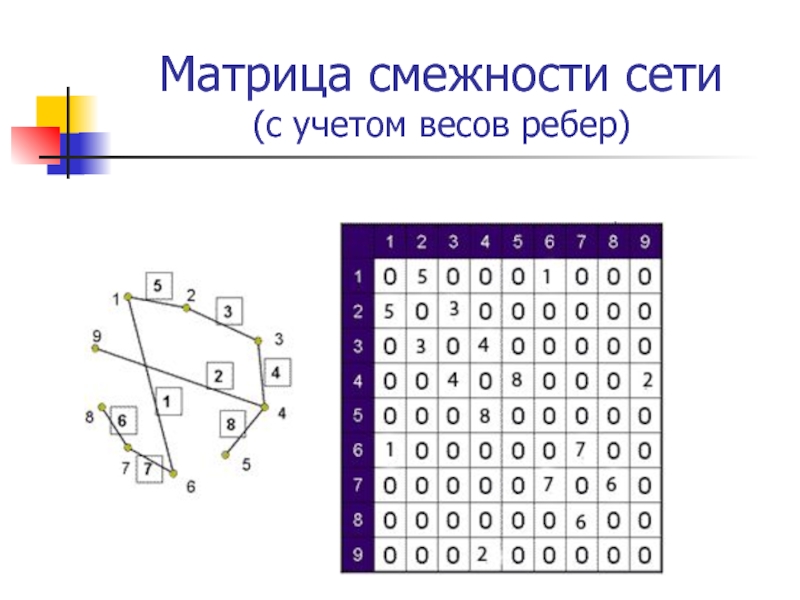
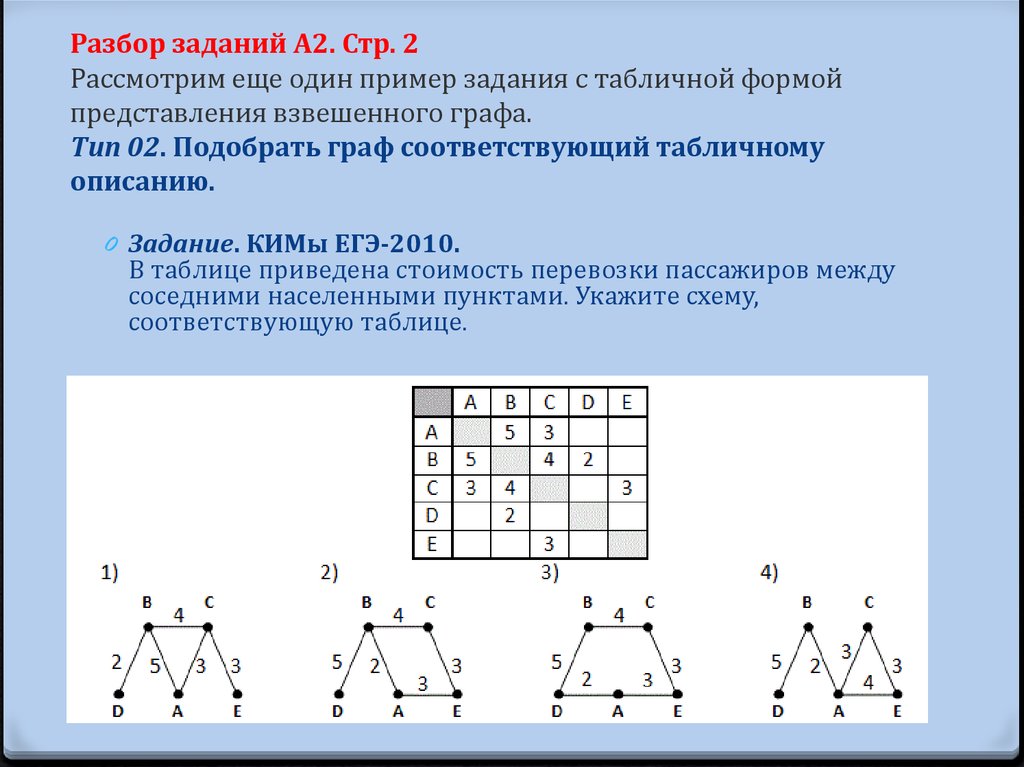
Используйте алгоритмы, такие как алгоритм Флойда-Уоршелла или Дейкстры, для нахождения кратчайших путей в графе на основе весовой матрицы.

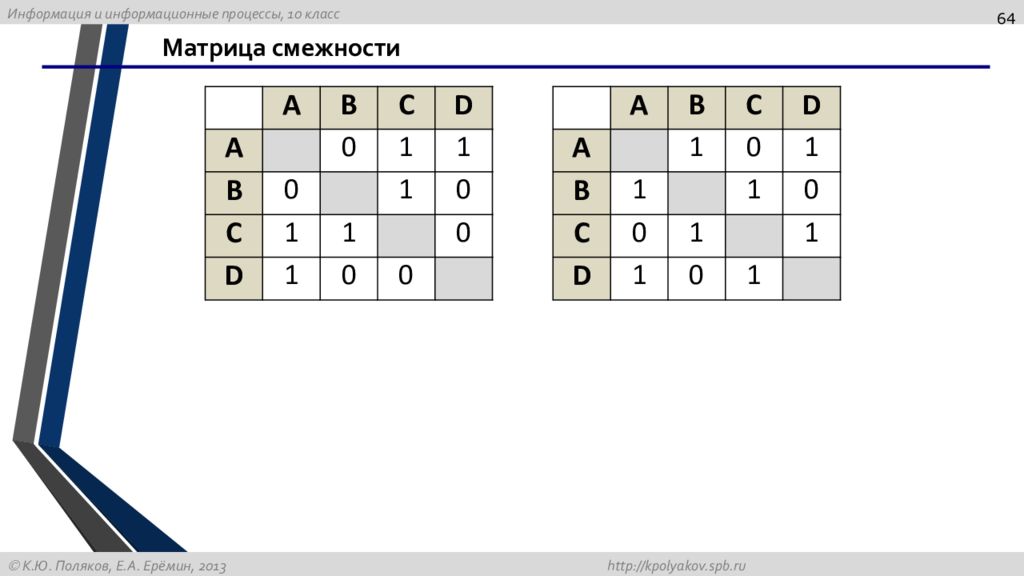
Обязательно проверяйте наличие циклов с отрицательным весом в графе, так как они могут привести к некорректным результатам при вычислении кратчайших путей.

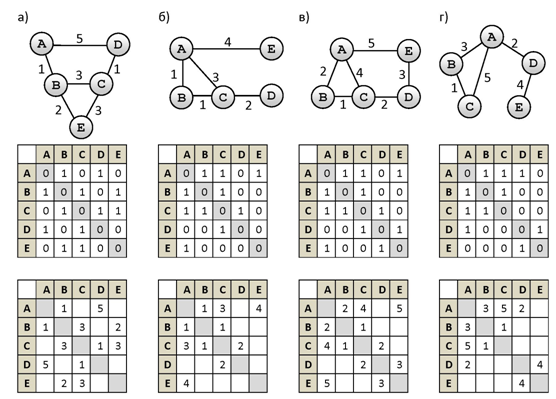
Для наглядности и удобства анализа графа можно визуализировать весовую матрицу с помощью специализированного ПО, такого как Graphviz.

При разработке приложений, работающих с графами, учитывайте масштабируемость и эффективность используемых структур данных и алгоритмов.

Используйте весовую матрицу для решения задач оптимизации, таких как нахождение минимального остовного дерева или максимального потока в сети.

Регулярно обновляйте весовую матрицу при изменении структуры графа или весов ребер, чтобы поддерживать актуальность данных.

Изучайте примеры и практические применения весовых матриц в различных областях, чтобы лучше понять их возможности и ограничения.