Как определять взаимное расположение прямой и окружности: полезные советы

Взаимное расположение прямой и окружности — важная тема в геометрии, которая помогает понять множество ключевых понятий и решать задачи. Эта страница включает фотографии и полезные советы для более глубокого понимания этого вопроса.

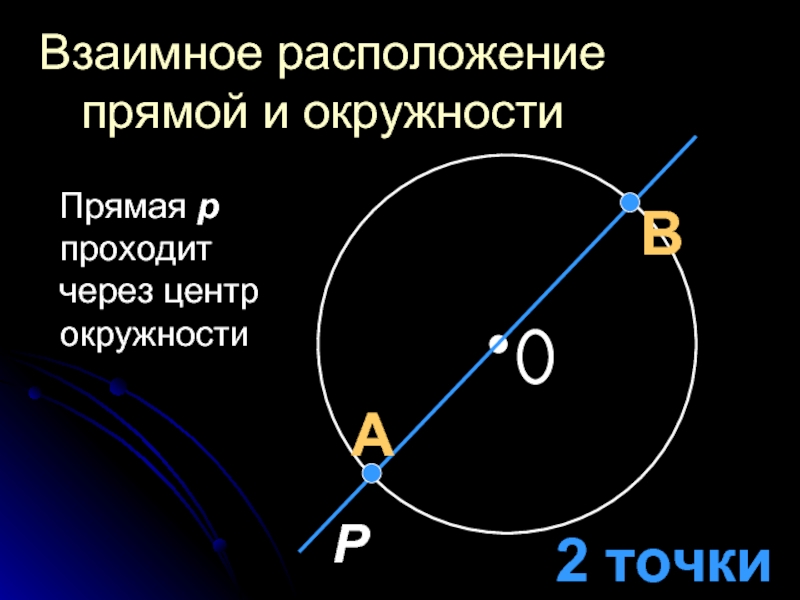
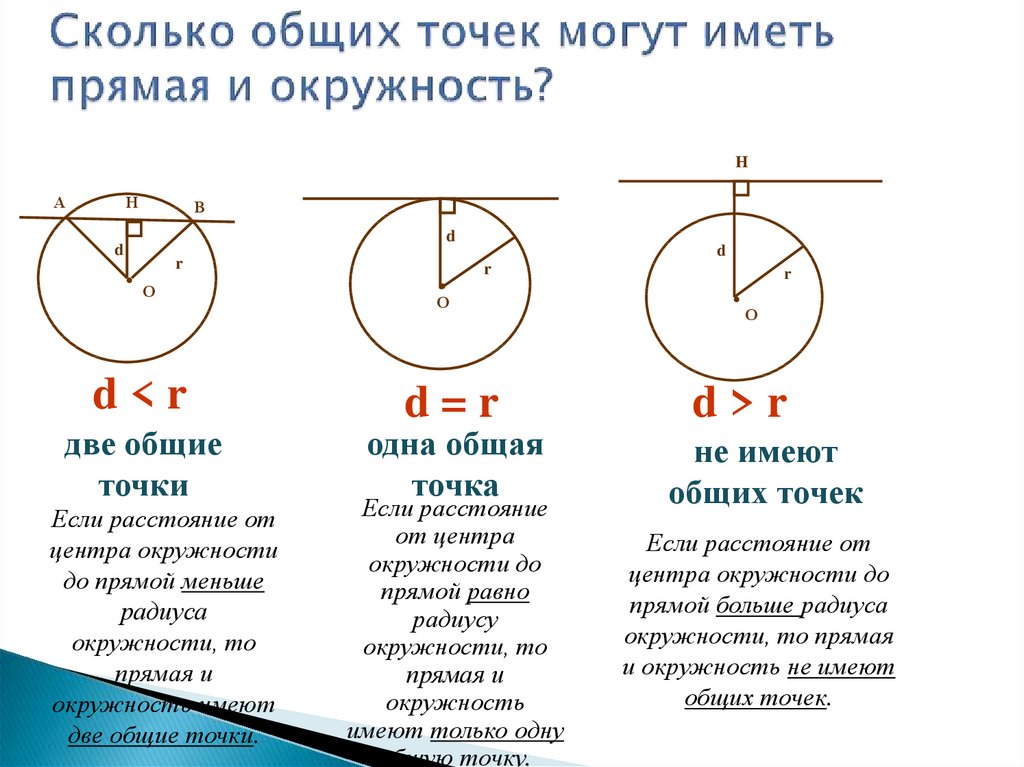
Для определения взаимного расположения прямой и окружности, начните с расчета расстояния от центра окружности до прямой.

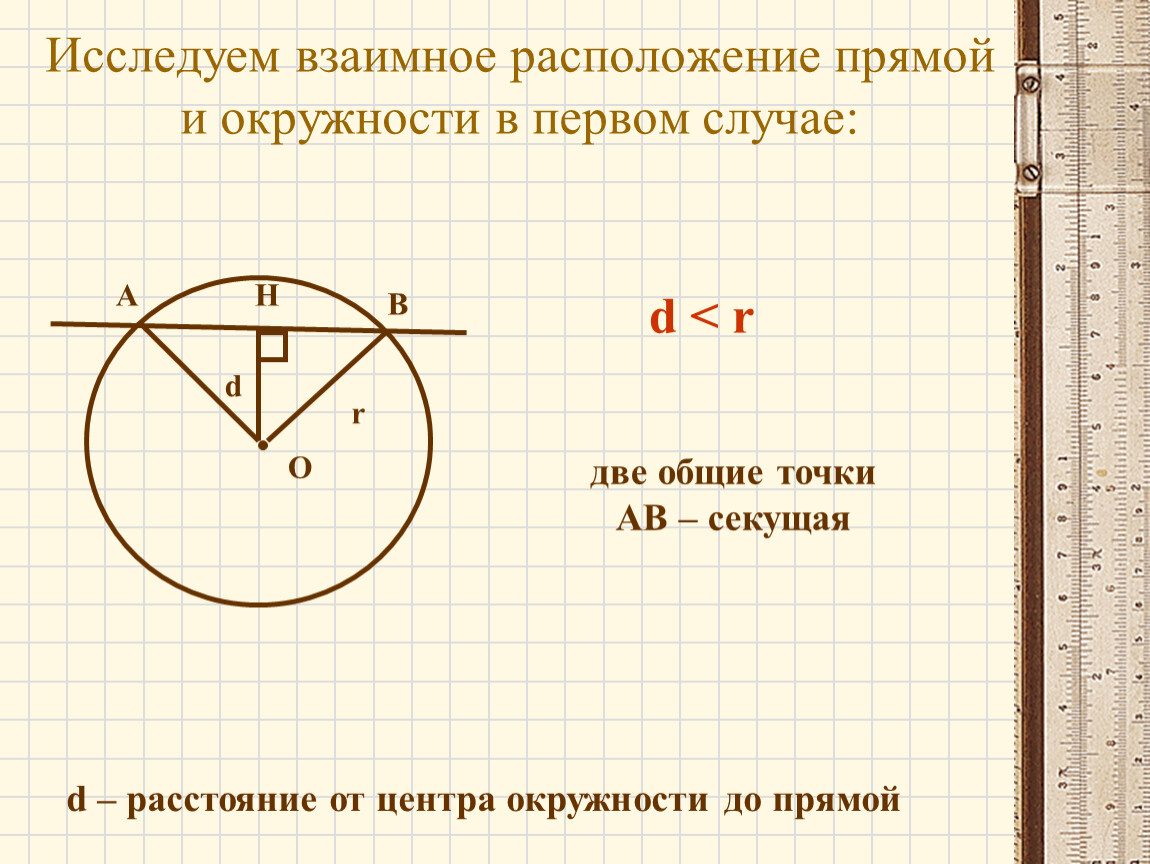
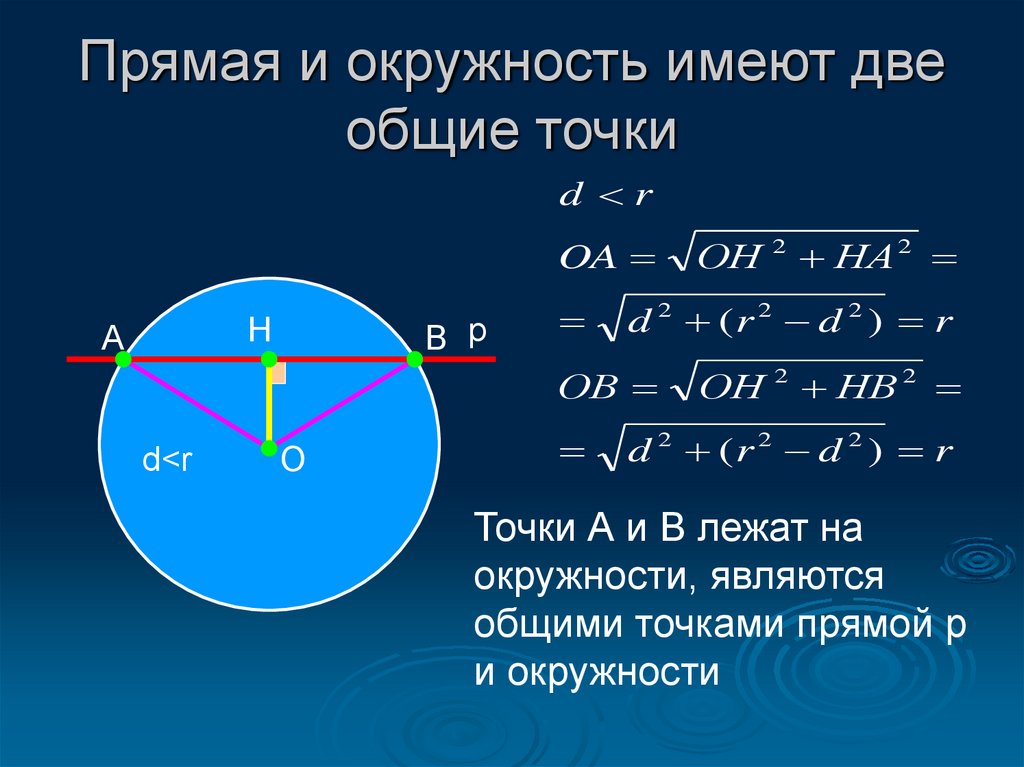
Если расстояние от центра окружности до прямой меньше радиуса окружности, прямая пересекает окружность в двух точках.

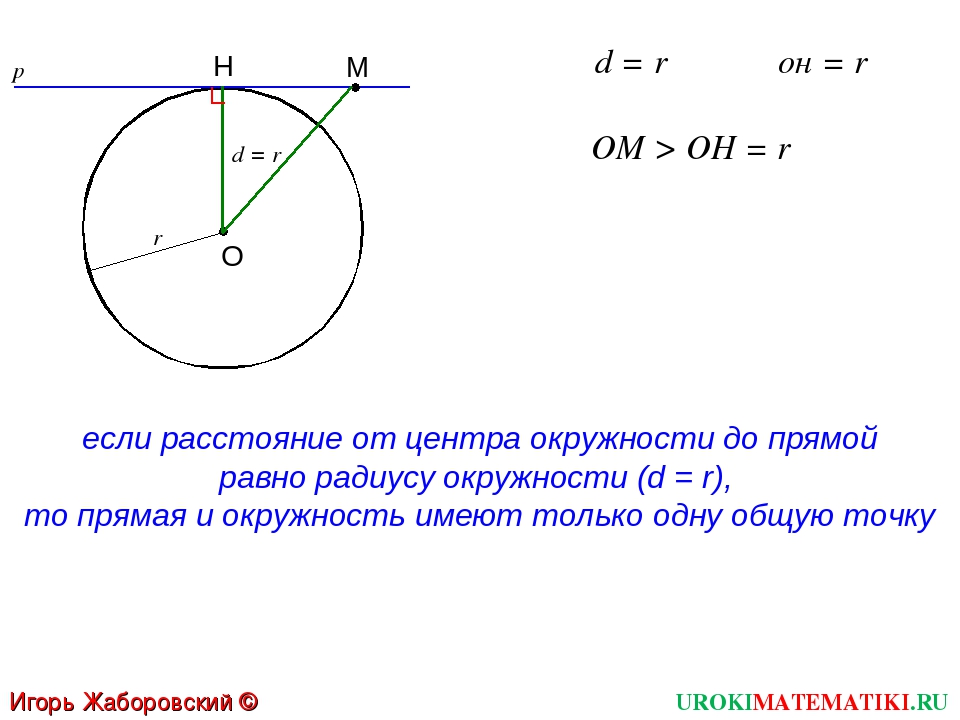
Если расстояние от центра окружности до прямой равно радиусу окружности, прямая касается окружности в одной точке.

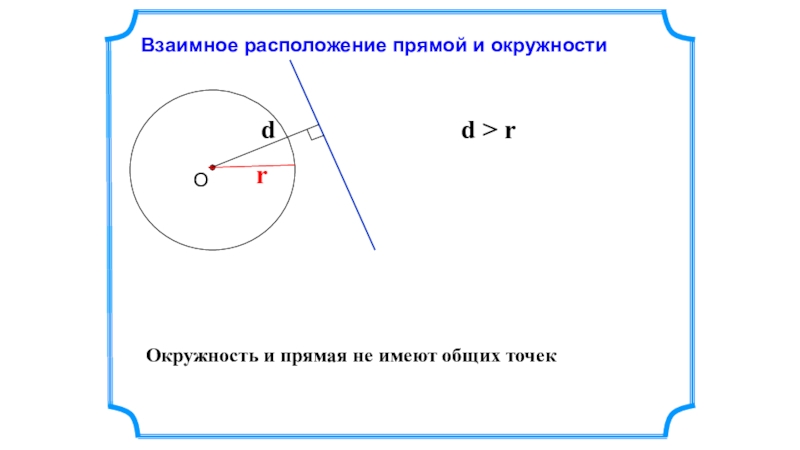
Если расстояние от центра окружности до прямой больше радиуса окружности, прямая не пересекает и не касается окружности.

Для нахождения точек пересечения используйте уравнения прямой и окружности, решая систему уравнений.

Не забудьте проверять дискриминант квадратного уравнения при решении системы уравнений: положительный дискриминант означает две точки пересечения, нулевой — одну, отрицательный — ни одной.

Используйте графическое представление для наглядного понимания взаимного расположения прямой и окружности.

Задачи на взаимное расположение прямой и окружности часто встречаются на экзаменах, поэтому практикуйте решение таких задач.

Применяйте теорему Пифагора для вычислений в задачах, связанных с прямыми и окружностями.

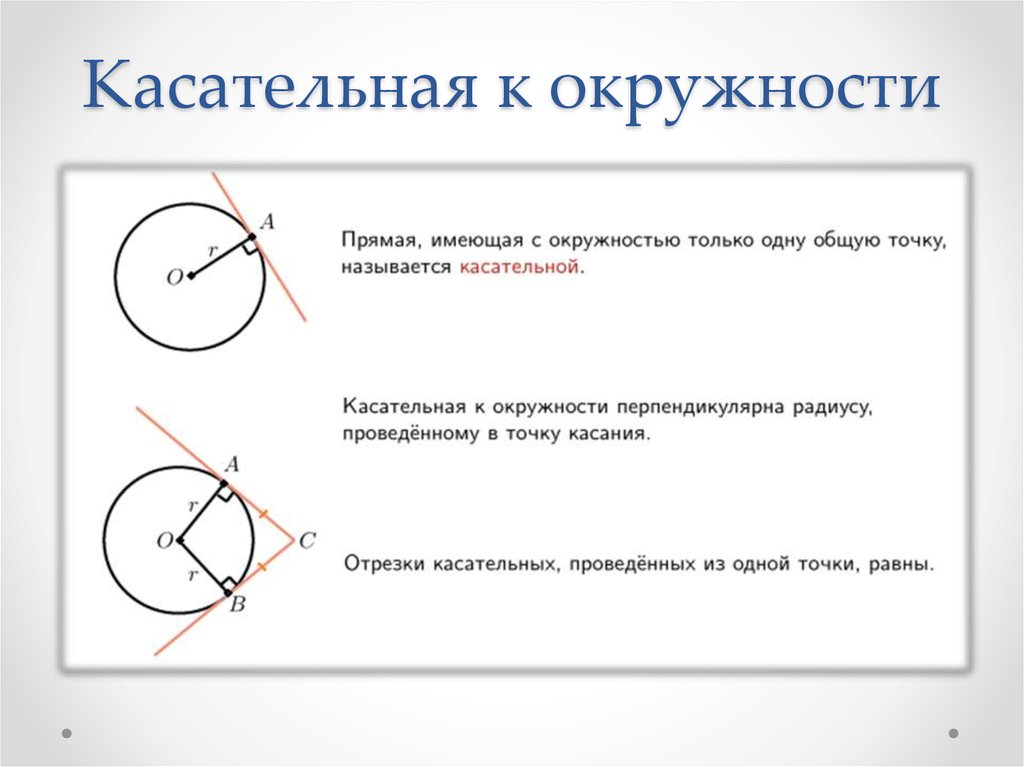
Помните, что точка касания прямой и окружности перпендикулярна радиусу, проведенному в этой точке.