Эффективные стратегии для доказательства свойств параллелограмма
На этой странице собраны полезные советы и примеры, которые помогут вам доказать, что данный четырехугольник является параллелограммом. Понимание свойств и методов доказательства параллелограммов является ключевым аспектом в изучении геометрии.
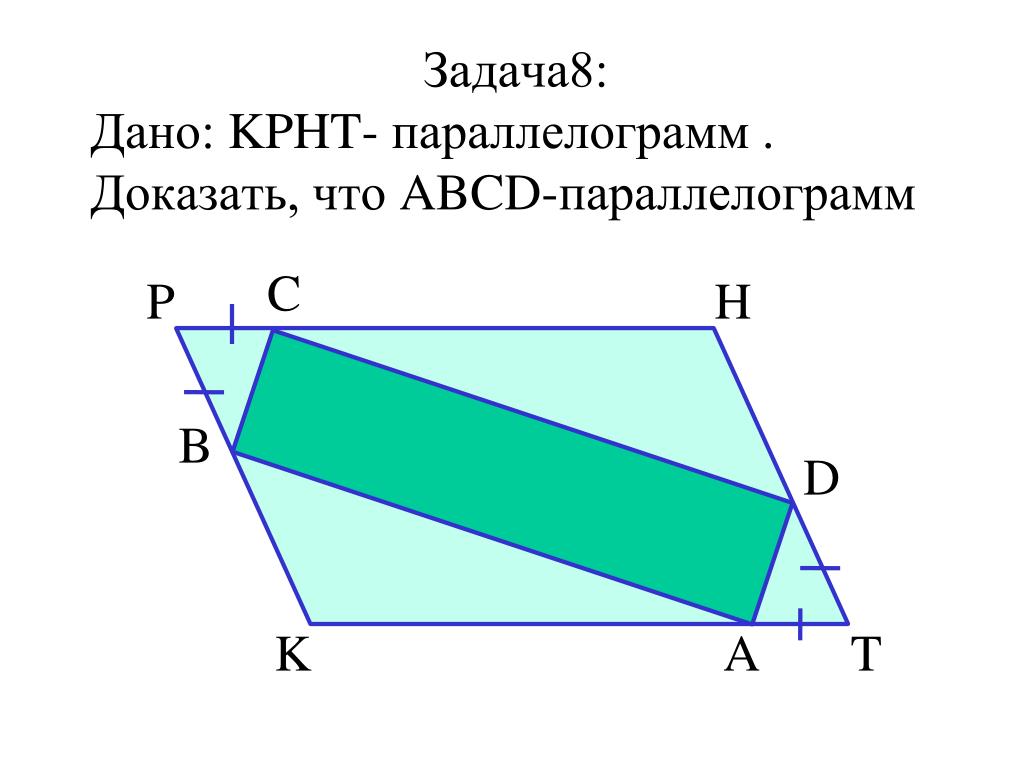
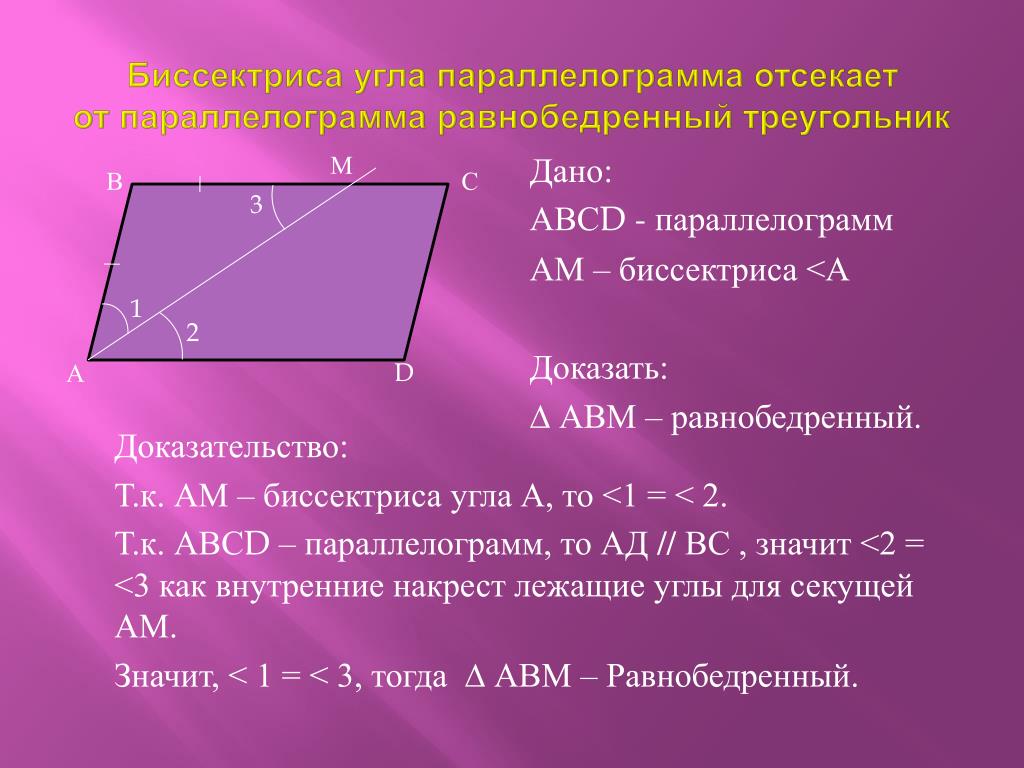
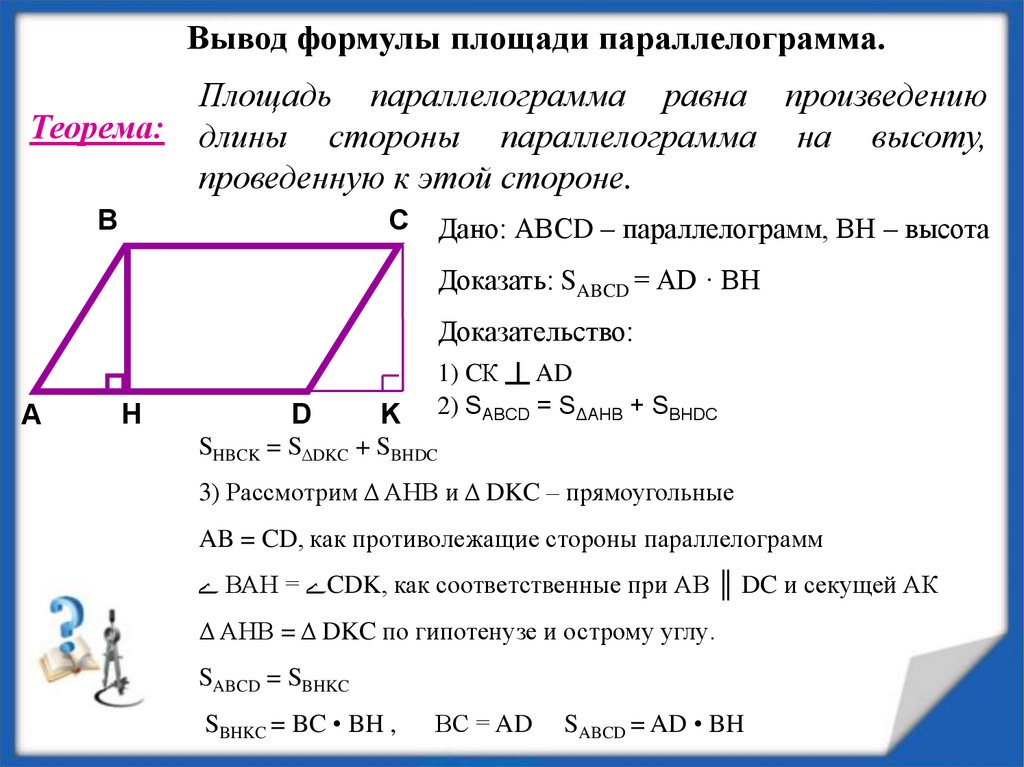
Проверяйте, равны ли противоположные стороны четырехугольника. Если да, то это параллелограмм.
Признаки параллелограмма Доказательство признаков параллелограмма
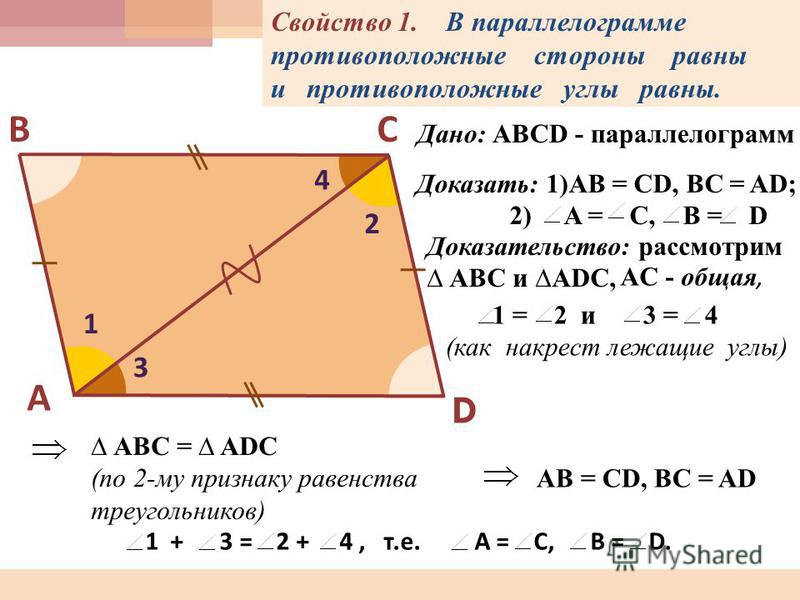
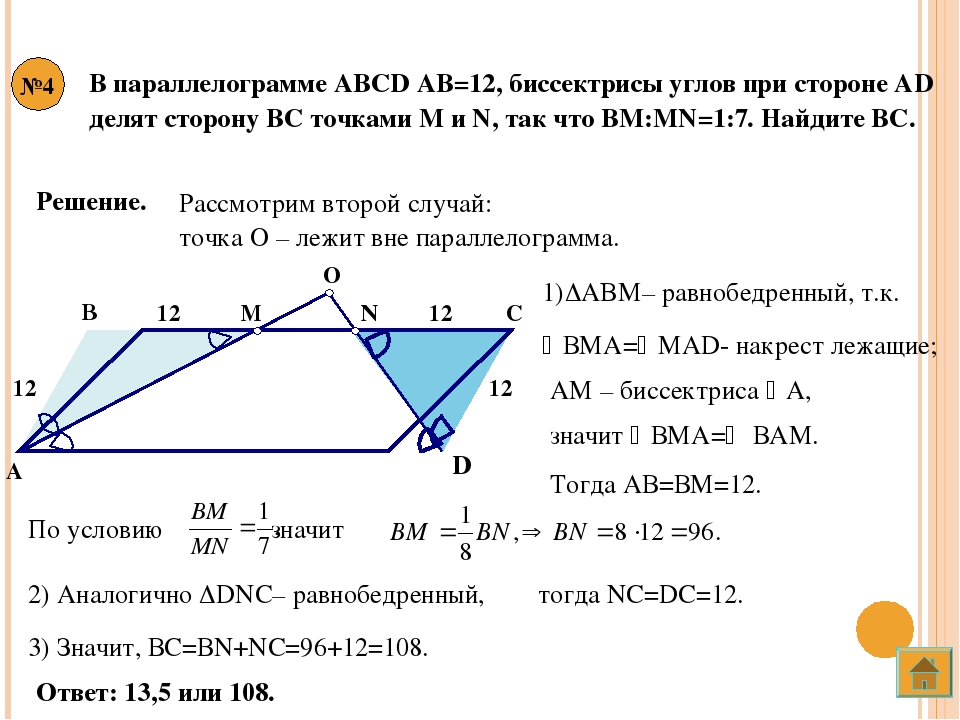
Используйте теорему о равенстве противоположных углов. Если они равны, то фигура – параллелограмм.
Свойства параллелограмма. Все задачи на периметр. Геометрия 8 класс
Убедитесь, что диагонали четырехугольника пересекаются и делятся пополам.
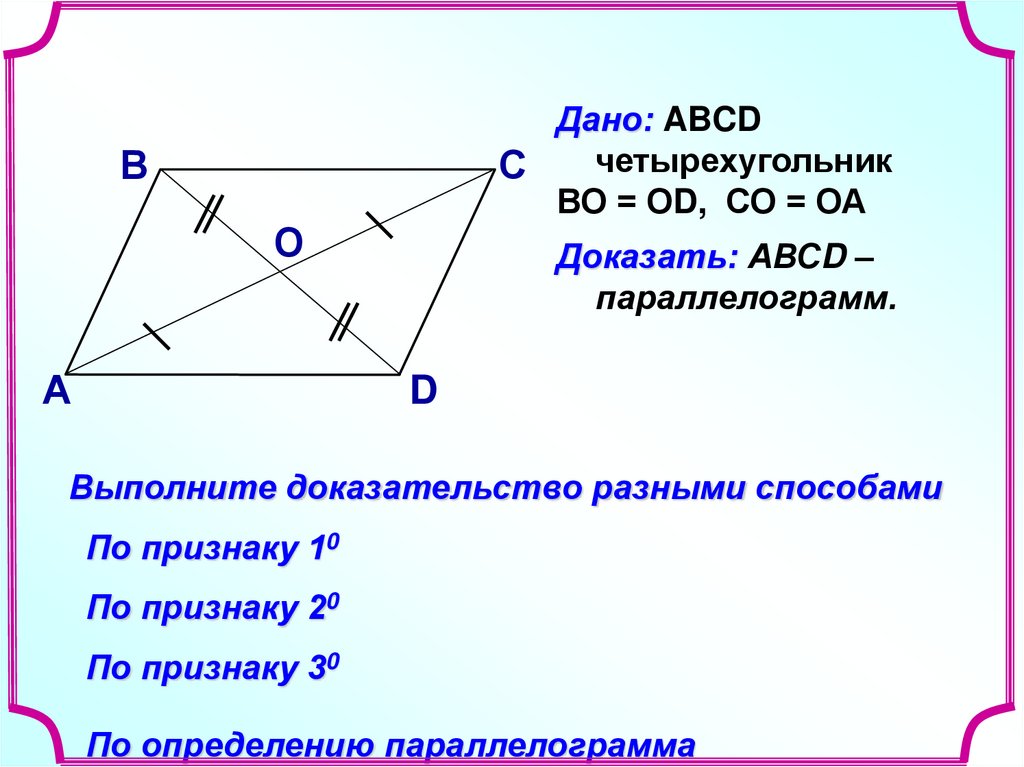
Проверяйте параллельность противоположных сторон с помощью углового измерения.
Параллелограмм. Практическая часть - решение задачи. 8 класс.
Если суммы углов, прилежащих к каждой стороне, равны 180 градусам, то это параллелограмм.


Используйте координатный метод для доказательства параллелограмма, проверяя равенство векторов.
При решении задач на плоскости, используйте свойство середины отрезка для определения параллелограмма.
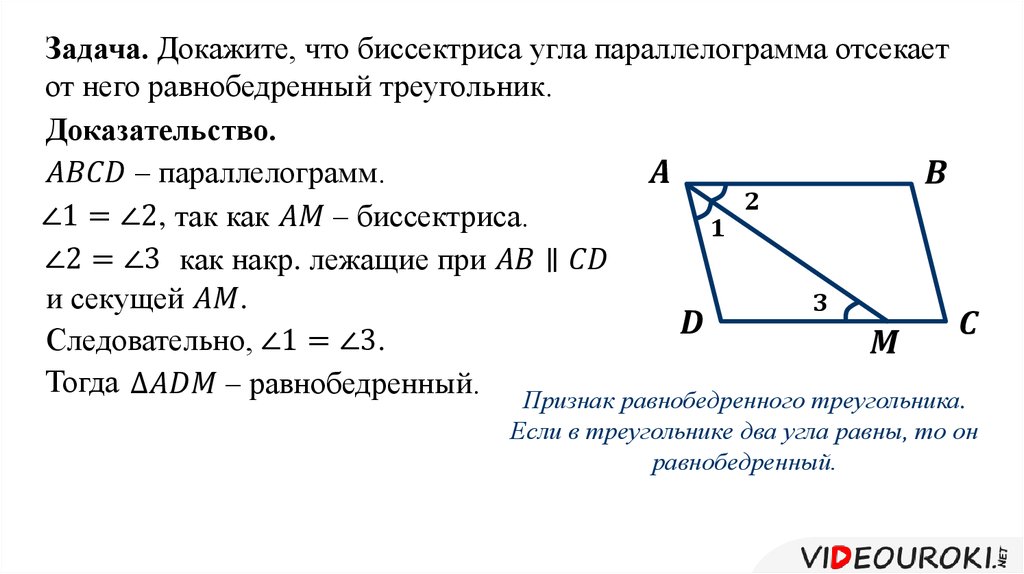
Докажите, что противоположные стороны четырехугольника равны и параллельны, используя формулы расстояний.
Применяйте теорему Пифагора для вычисления длины сторон и диагоналей четырехугольника.
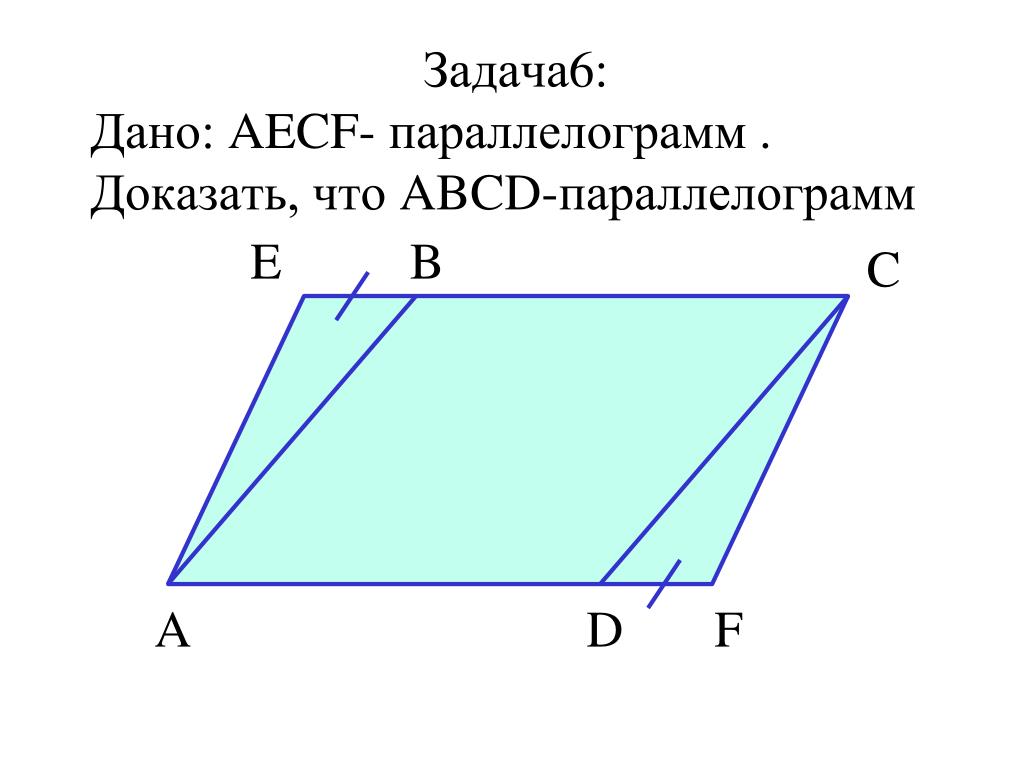
Используйте графические методы для построения и проверки свойств параллелограмма на бумаге или в программе.