Основные советы по решению геометрических задач: медианы, биссектрисы и высоты

На этой странице вы найдете полезные советы и рекомендации по решению задач по геометрии, связанных с медианами, биссектрисами и высотами треугольников. Мы рассмотрим ключевые понятия, методы и подходы, которые помогут вам успешно справляться с задачами на экзаменах и в учебе.

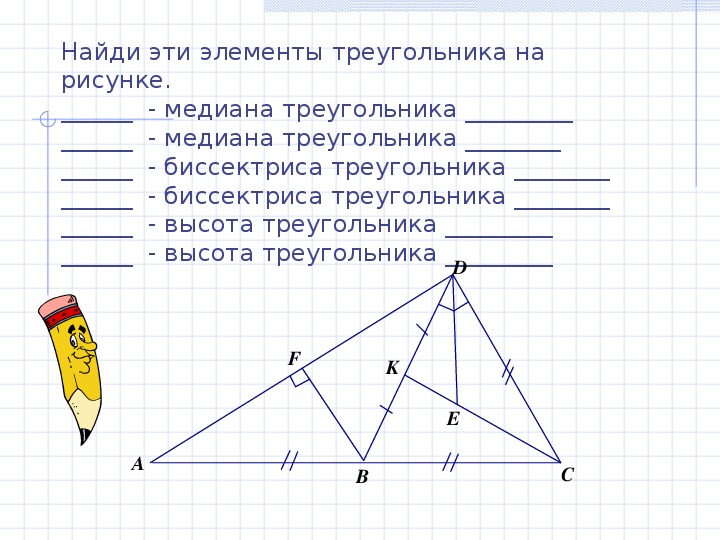
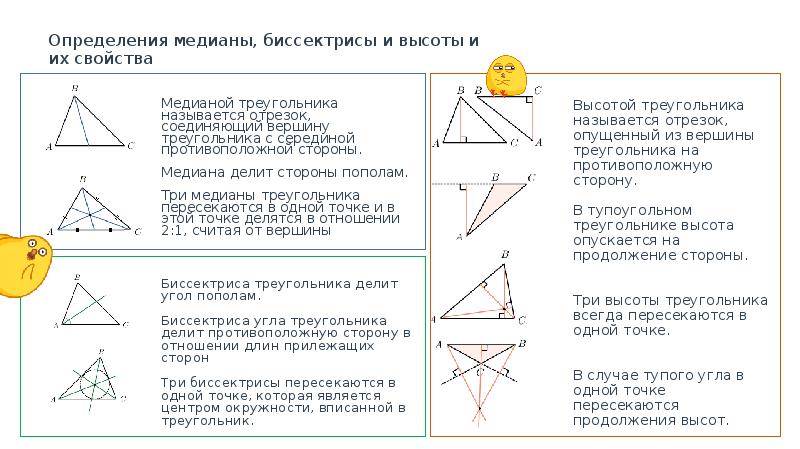
При работе с медианами треугольника помните, что медиана делит треугольник на два равных по площади треугольника.

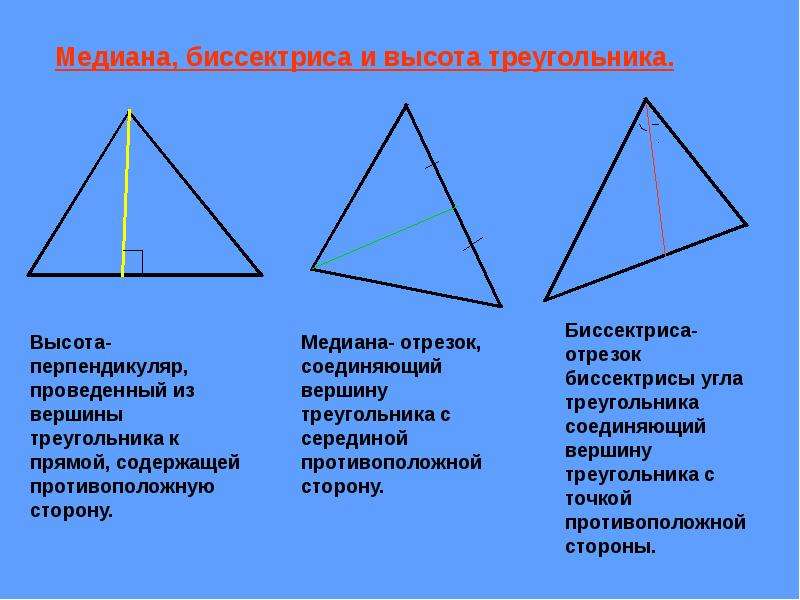
Биссектрисы треугольника пересекаются в одной точке, которая называется центром вписанной окружности.

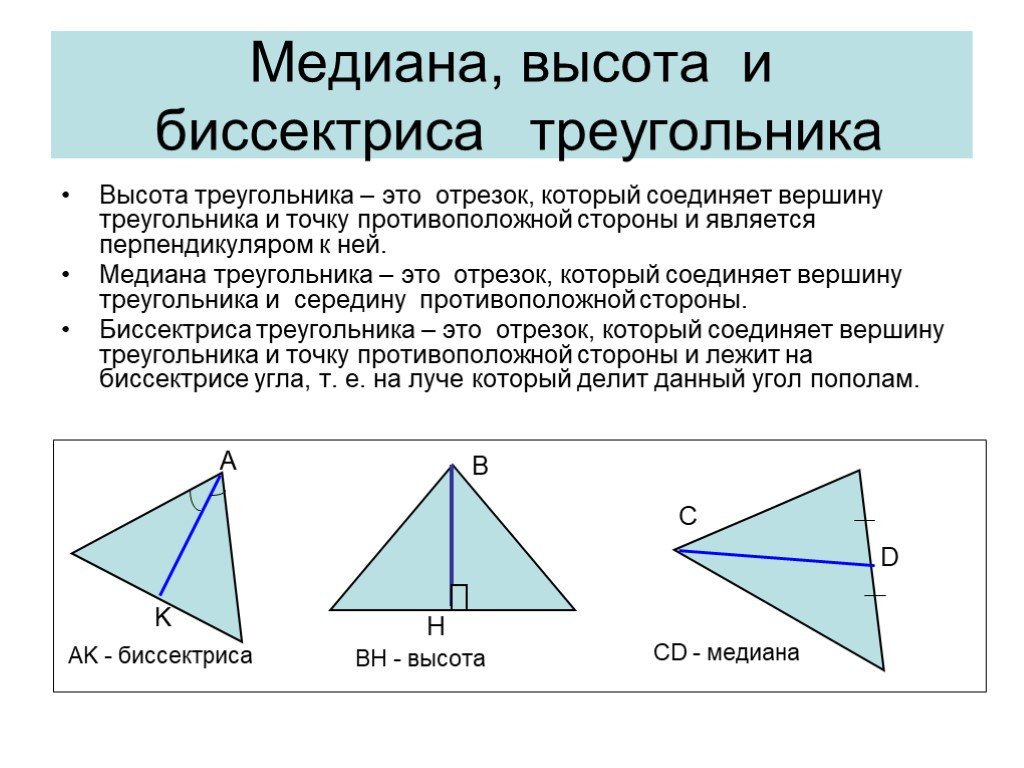
Высота треугольника всегда перпендикулярна основанию и может быть проведена из любой вершины треугольника.

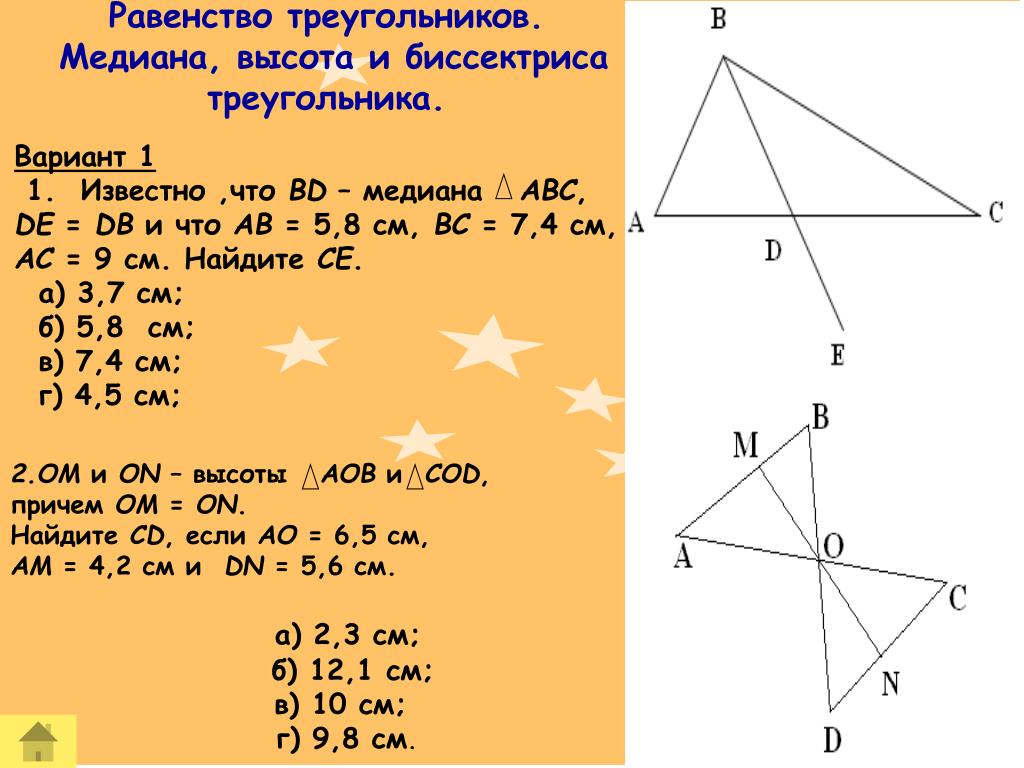
Используйте теорему о медианах, чтобы найти длину медианы, зная стороны треугольника.

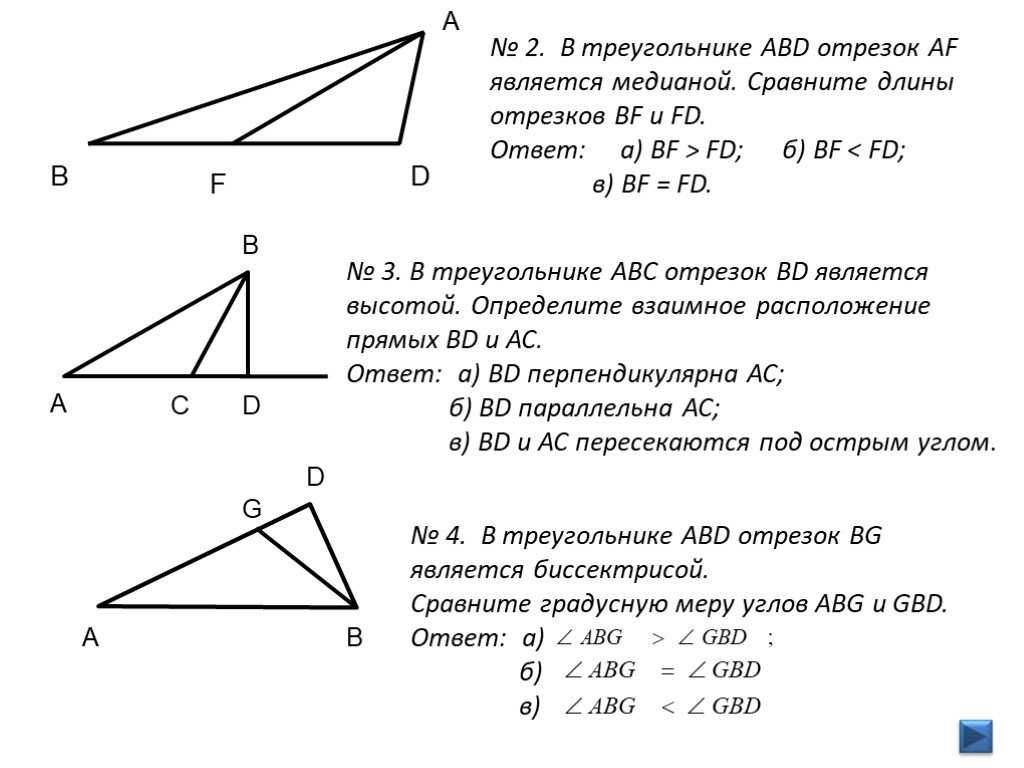
Чтобы вычислить угол между двумя медианами, используйте свойства параллельных и пересекающихся прямых в треугольнике.

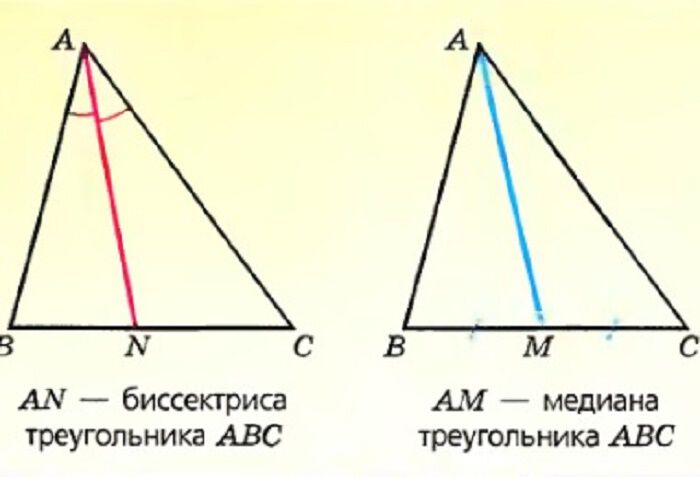
Помните, что в равнобедренном треугольнике биссектрисы углов равны между собой.

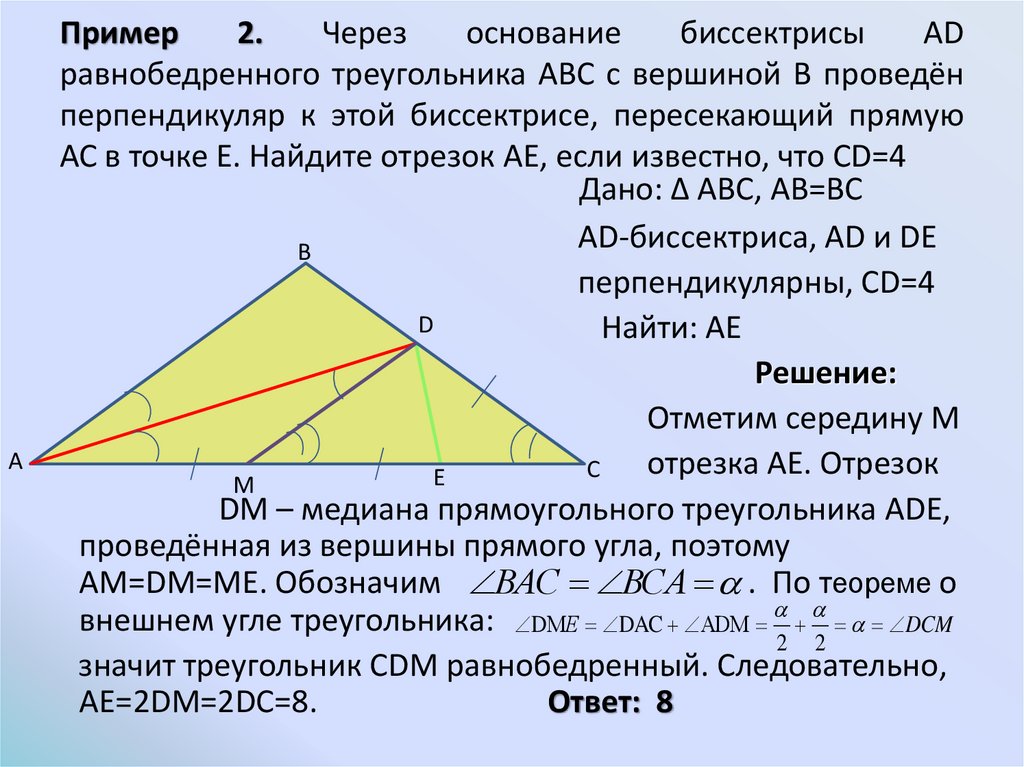
При решении задач на высоты треугольника используйте формулу площади через высоту и основание.

Для нахождения точки пересечения биссектрис используйте свойства углов и треугольников.

Используйте симметрию треугольника для упрощения расчетов при работе с медианами и высотами.

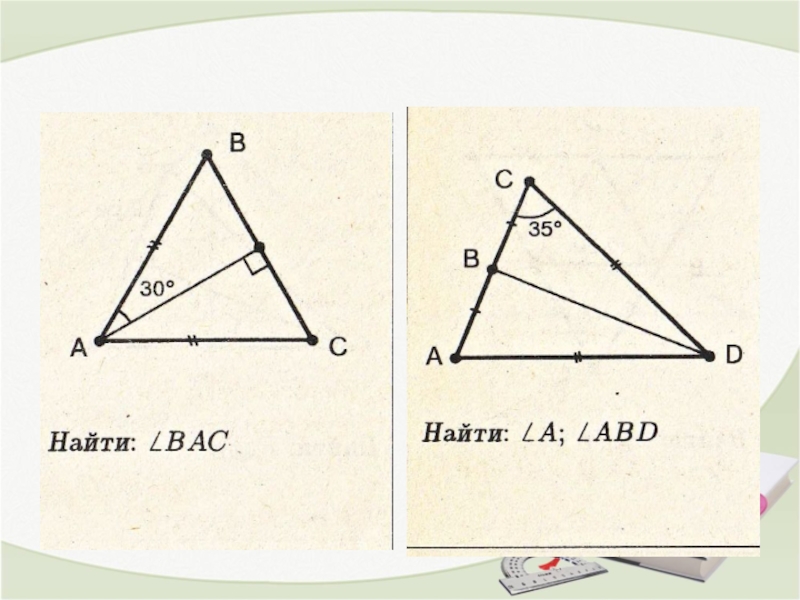
Проанализируйте различные способы нахождения медиан, высот и биссектрис в треугольниках, чтобы выбрать наиболее подходящий метод для задачи.