Как построить гиперболу: пошаговое руководство
Гипербола — это одна из конических сечений, представляющая собой график функции, имеющий форму двух симметричных ветвей. В этой статье вы найдете подробное описание построения графика гиперболы и основные формулы, необходимые для работы с этим математическим объектом.
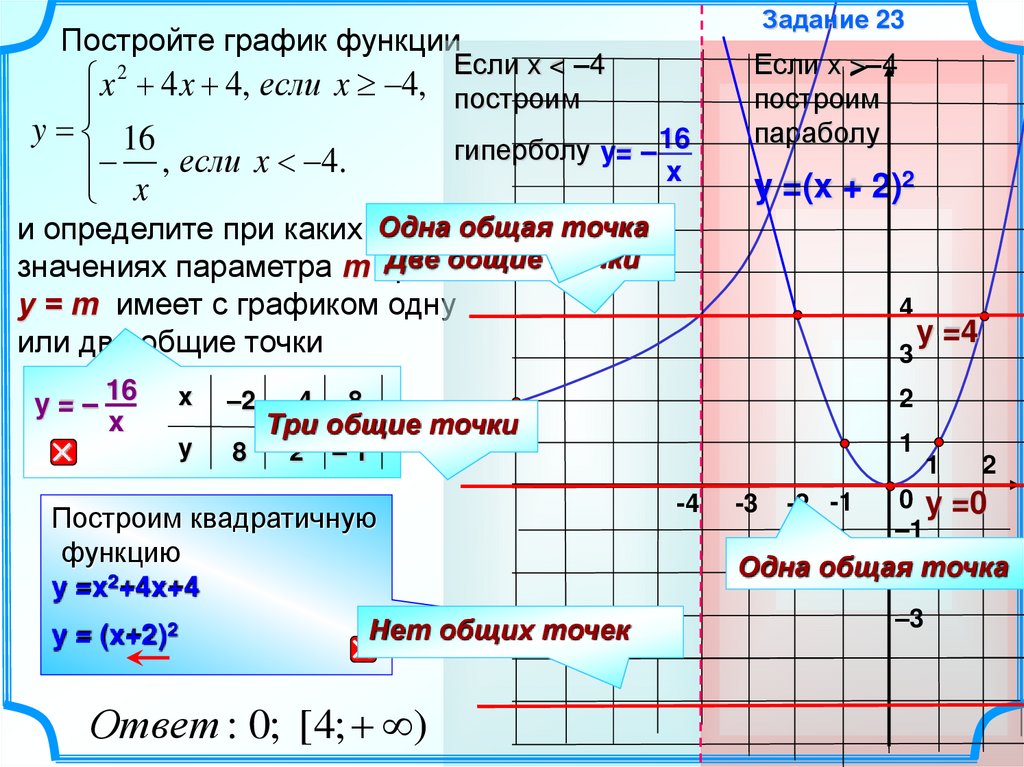

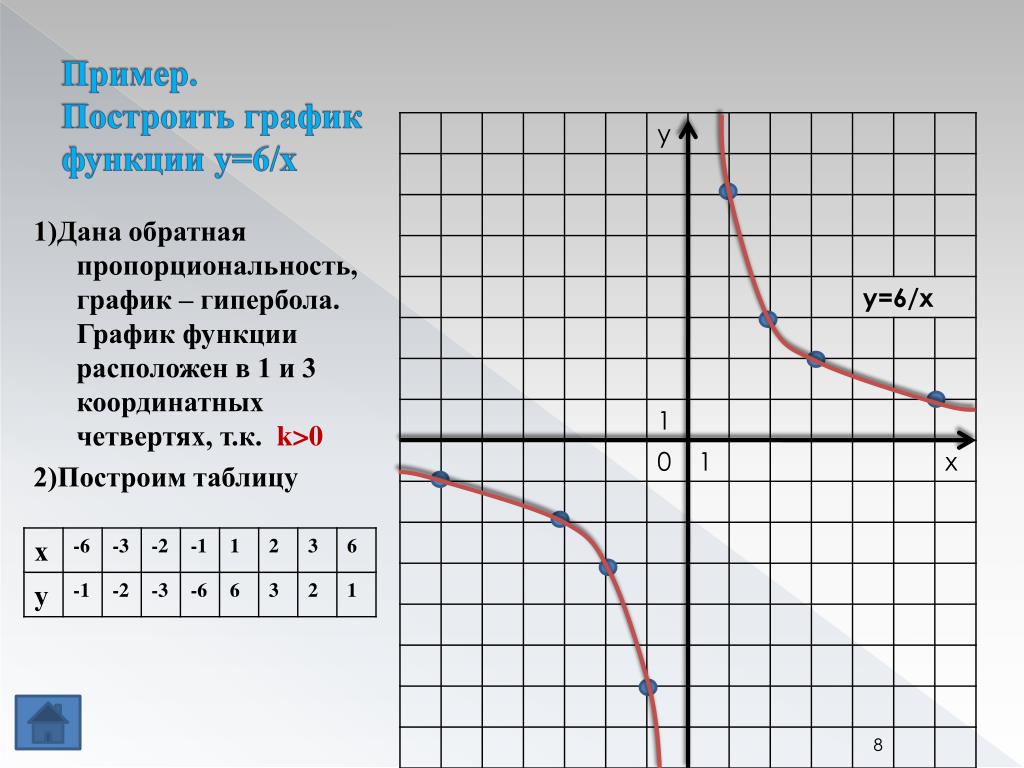
Начните с определения уравнения гиперболы в стандартной форме: (x^2/a^2) - (y^2/b^2) = 1 или (y^2/a^2) - (x^2/b^2) = 1.
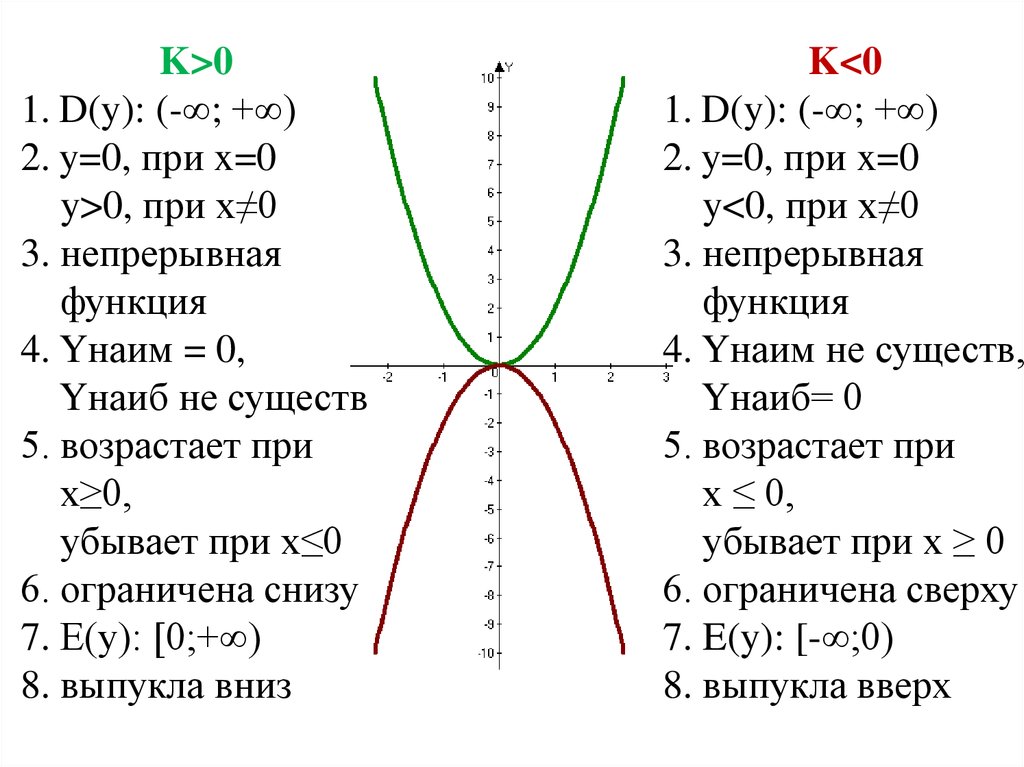

Определите центр гиперболы, который находится в точке (h, k) для уравнений с учетом смещения: ((x-h)^2/a^2) - ((y-k)^2/b^2) = 1.
Как построить график линейной функции.
Найдите вершины гиперболы, которые располагаются на расстоянии a от центра вдоль оси симметрии.

Рассчитайте фокусы гиперболы, используя формулу c^2 = a^2 + b^2, где c — расстояние от центра до фокуса.
Формула гиперболы по рисунку
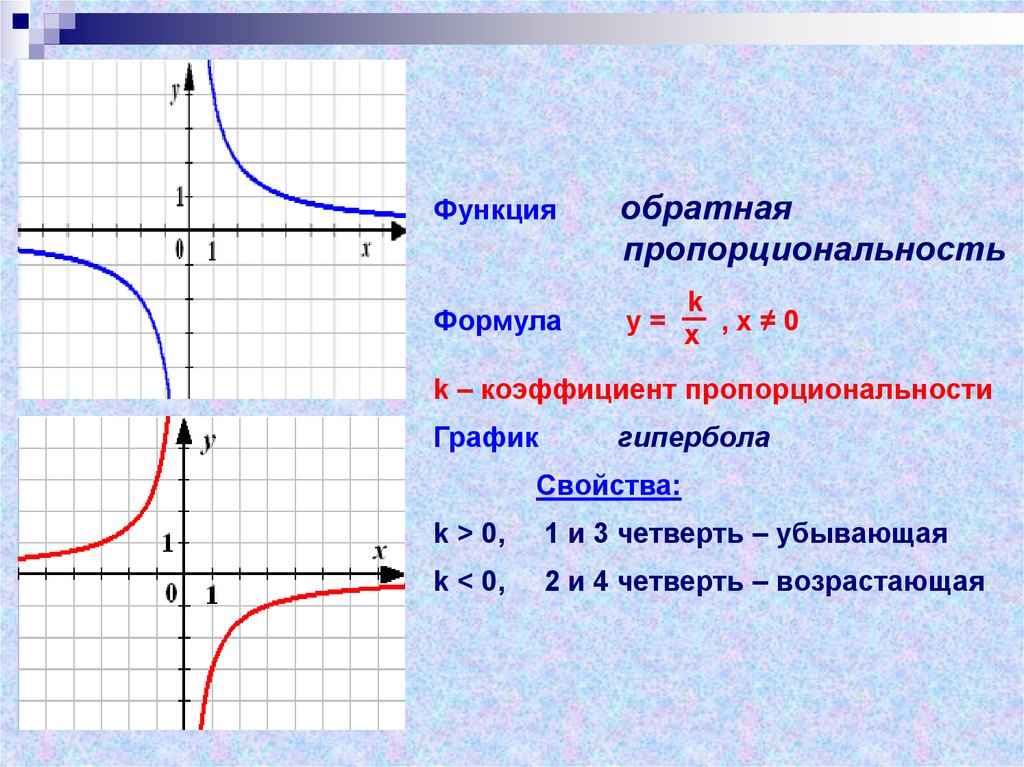
Постройте асимптоты гиперболы, которые проходят через центр и имеют угловые коэффициенты ±(b/a) или ±(a/b).
Уравнение гиперболы в задании первой части профильного ЕГЭ по математике
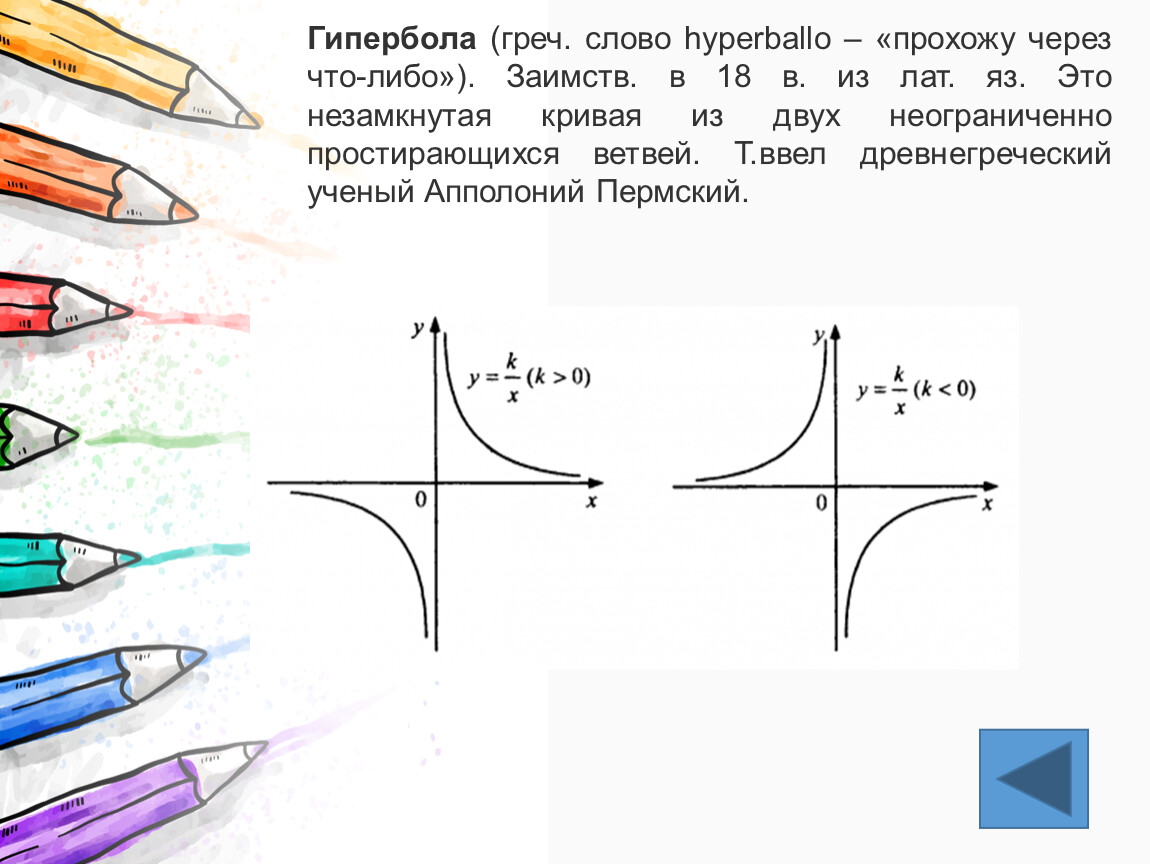
Используйте асимптоты как направляющие линии для точного построения ветвей гиперболы.
Отметьте точки пересечения гиперболы с осями координат, если таковые существуют, для дополнительной точности графика.
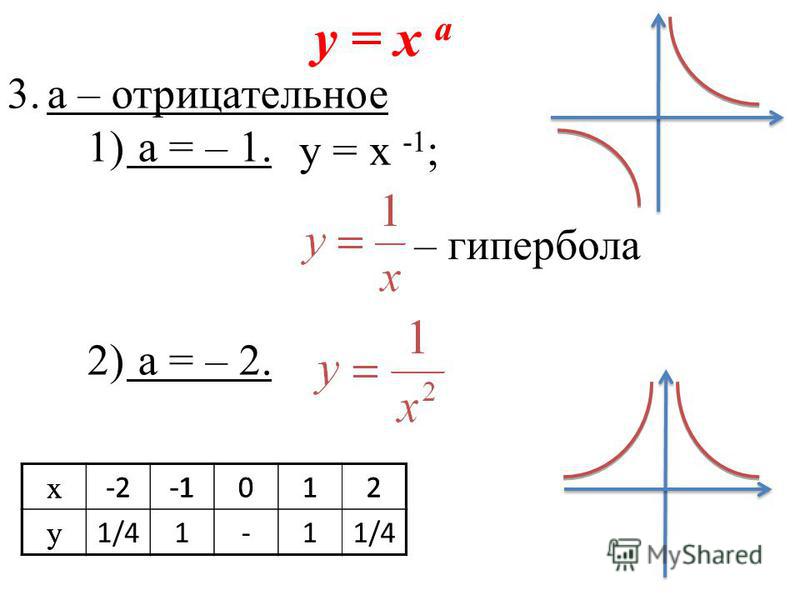
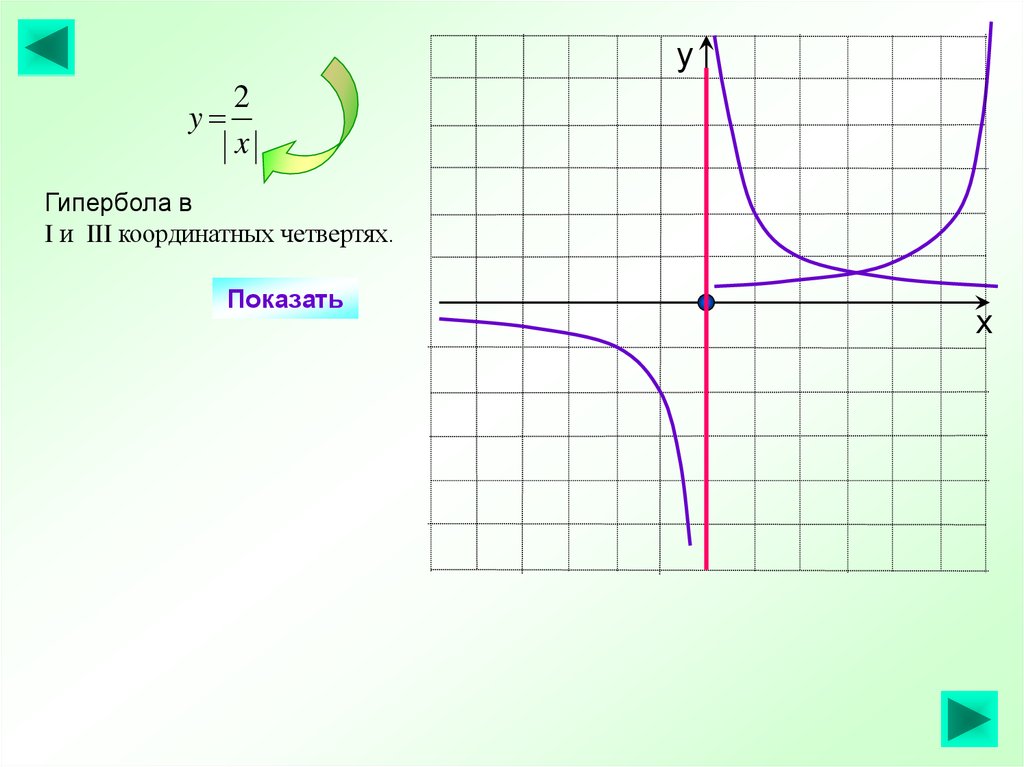
Постройте вспомогательные прямоугольники, стороны которых параллельны осям координат и проходят через вершины гиперболы.
Обратите внимание на симметрию гиперболы относительно осей и центра при построении графика.
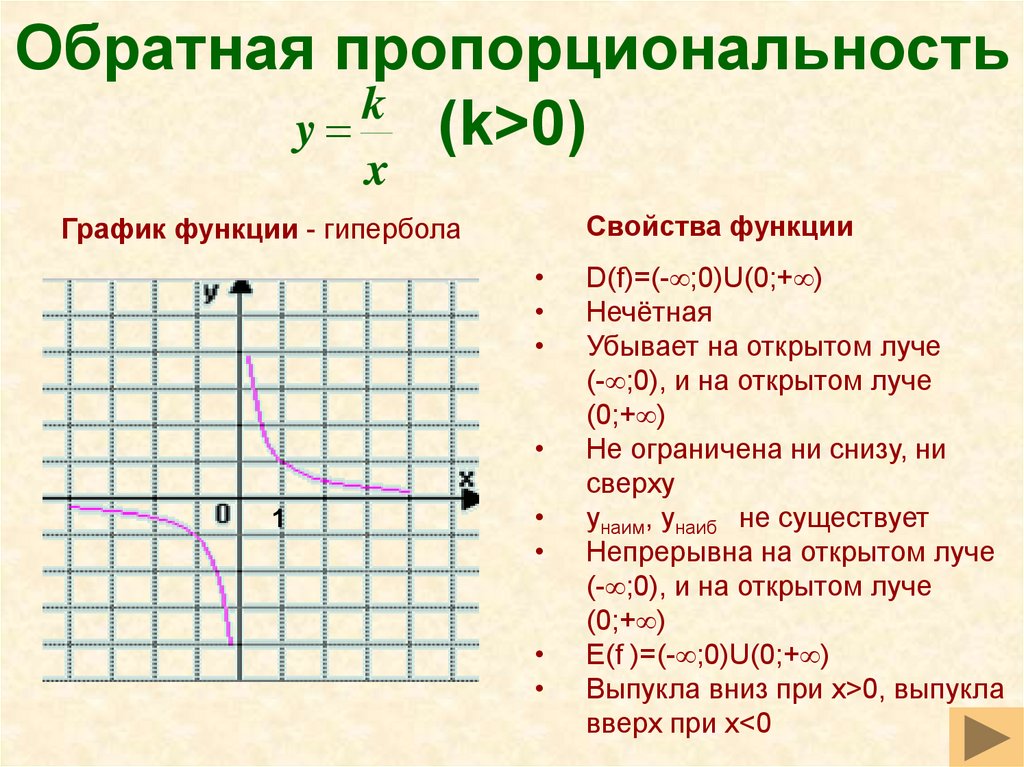
ОГЭ 2022. Задание 11. Сопоставить функции и графики. Обратная пропорциональность. Гипербола
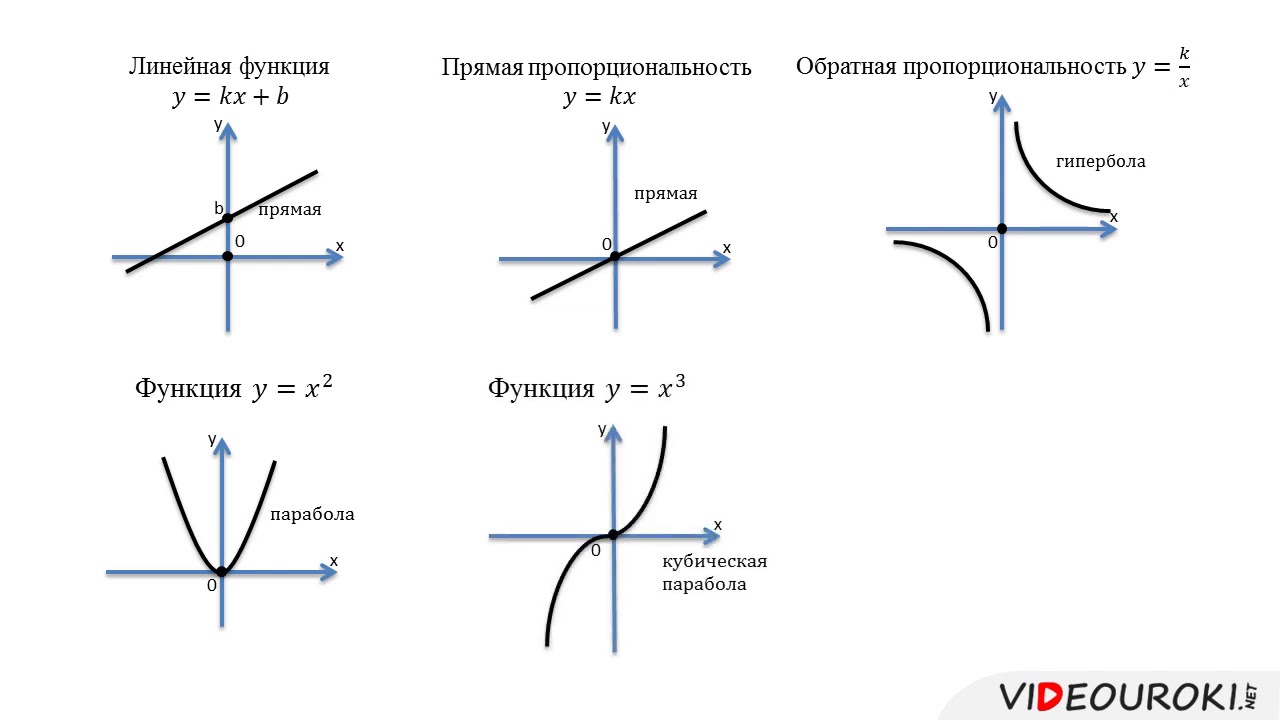
Проверяйте точность построения, сравнивая полученные результаты с исходными формулами и уравнениями.