Производная функции на графике: объяснение и примеры

На этой странице вы найдете подборку фотографий и полезные советы, которые помогут вам лучше понять, как работает производная функции на графике. Производная - важный инструмент в математике, который позволяет анализировать изменения функции и их скорость.

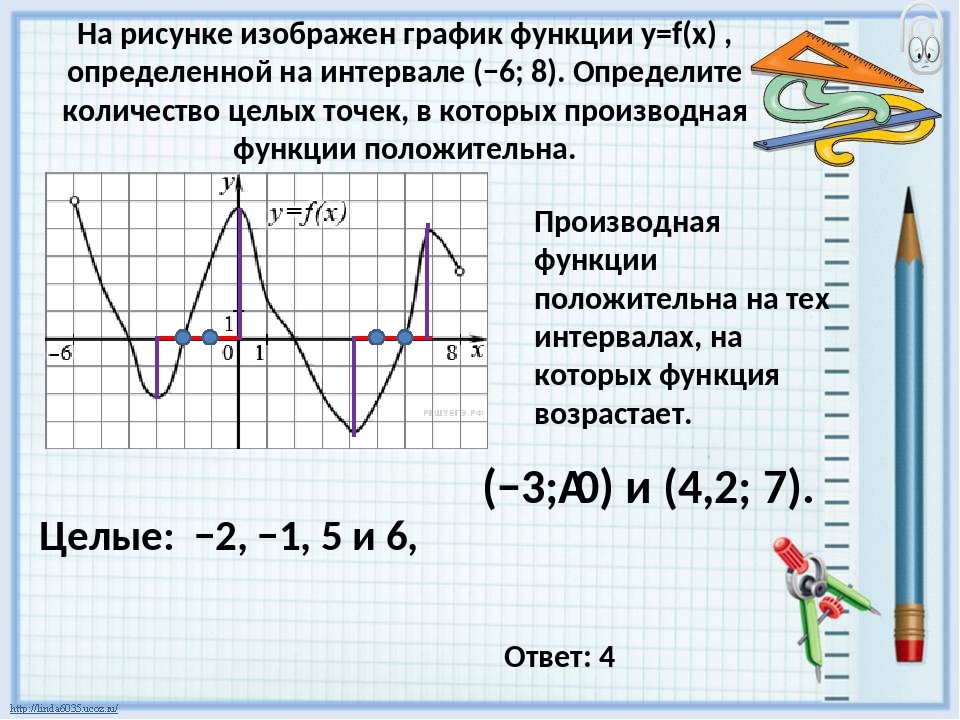
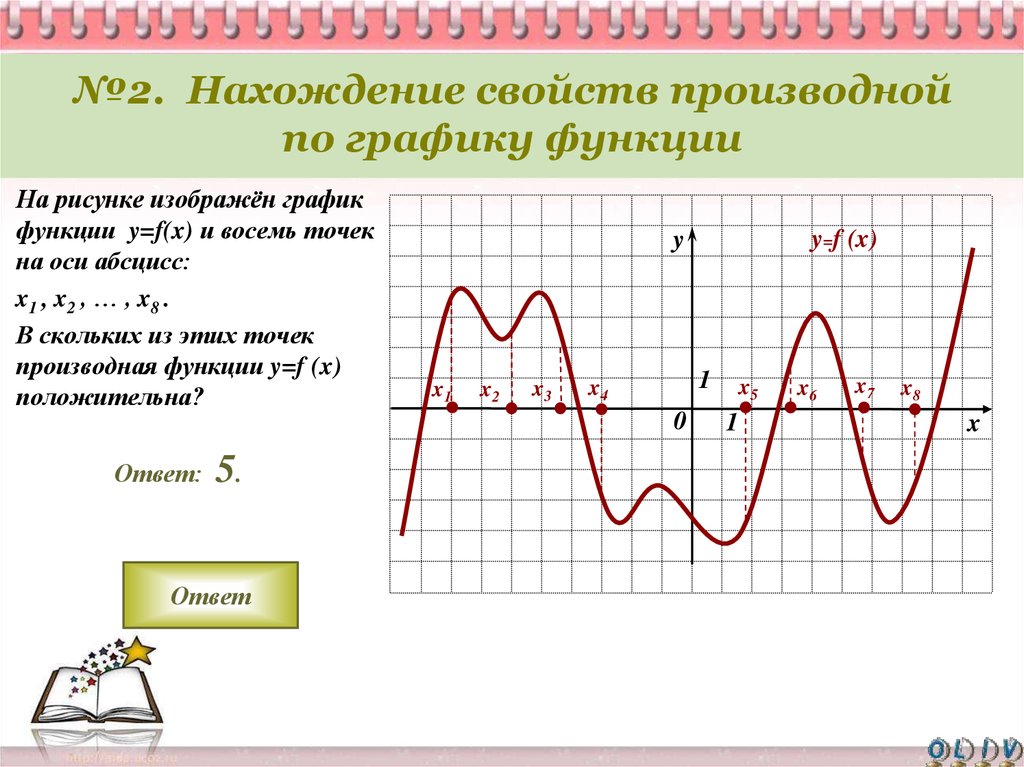
Изучите основные правила нахождения производной: правила дифференцирования, такие как правило произведения и правило цепочки, помогут вам найти производные сложных функций.

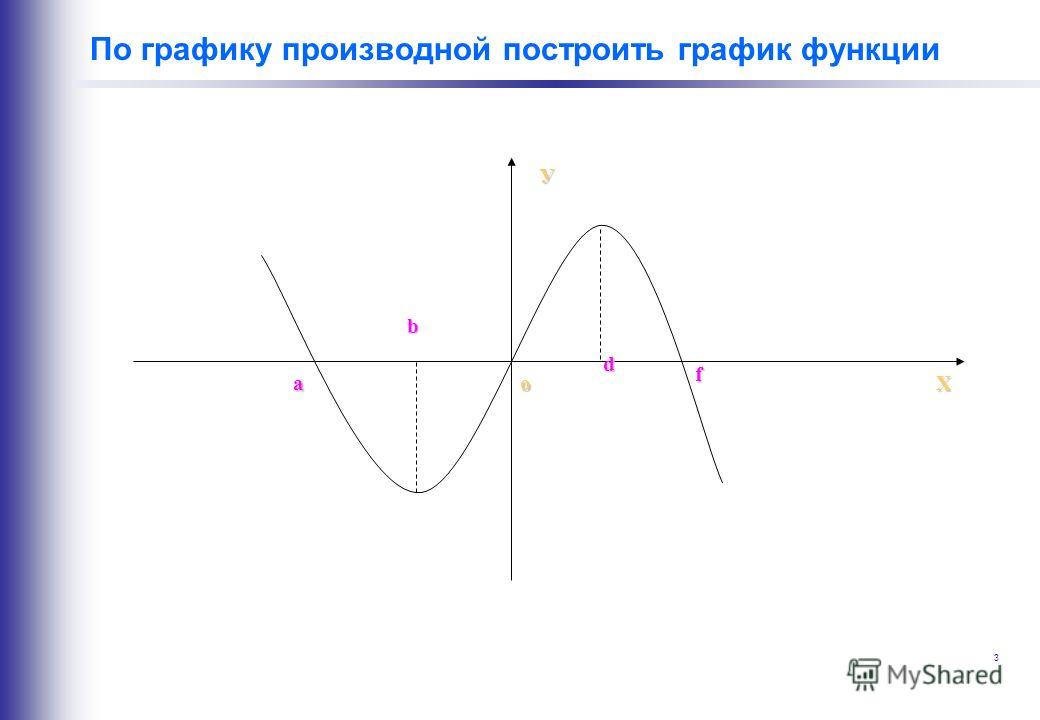
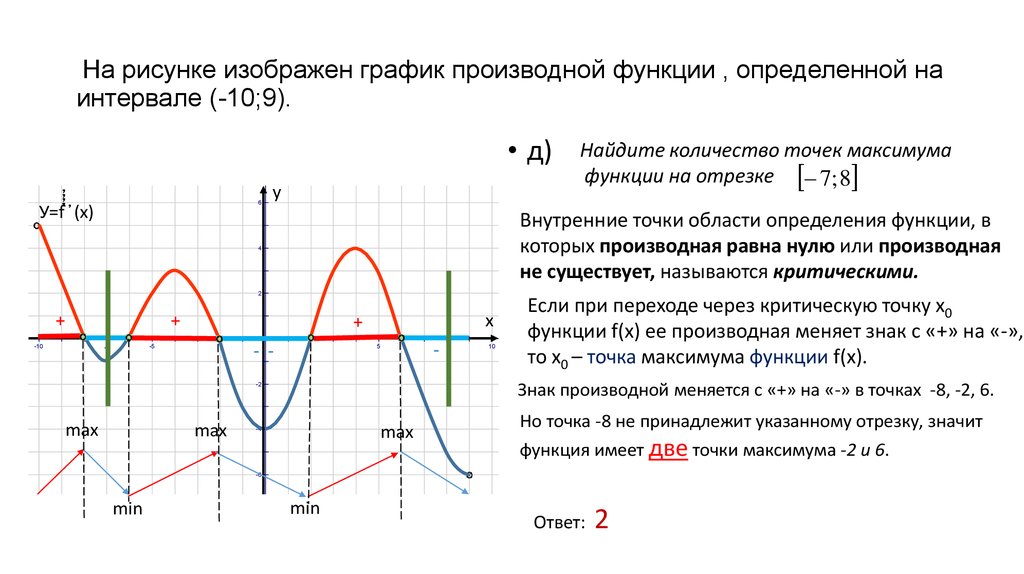
Практикуйтесь на простых примерах: начните с базовых функций, таких как линейные и квадратичные, прежде чем переходить к более сложным.

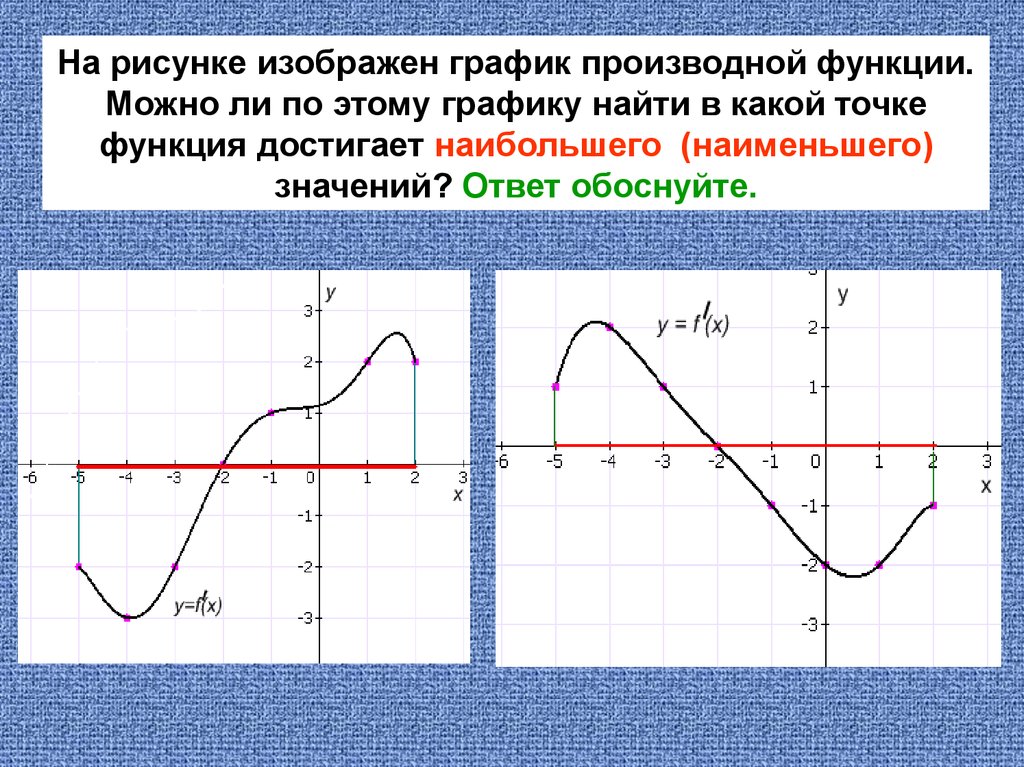
Используйте графики для визуализации: графическое представление функции и ее производной поможет лучше понять взаимосвязь между ними.

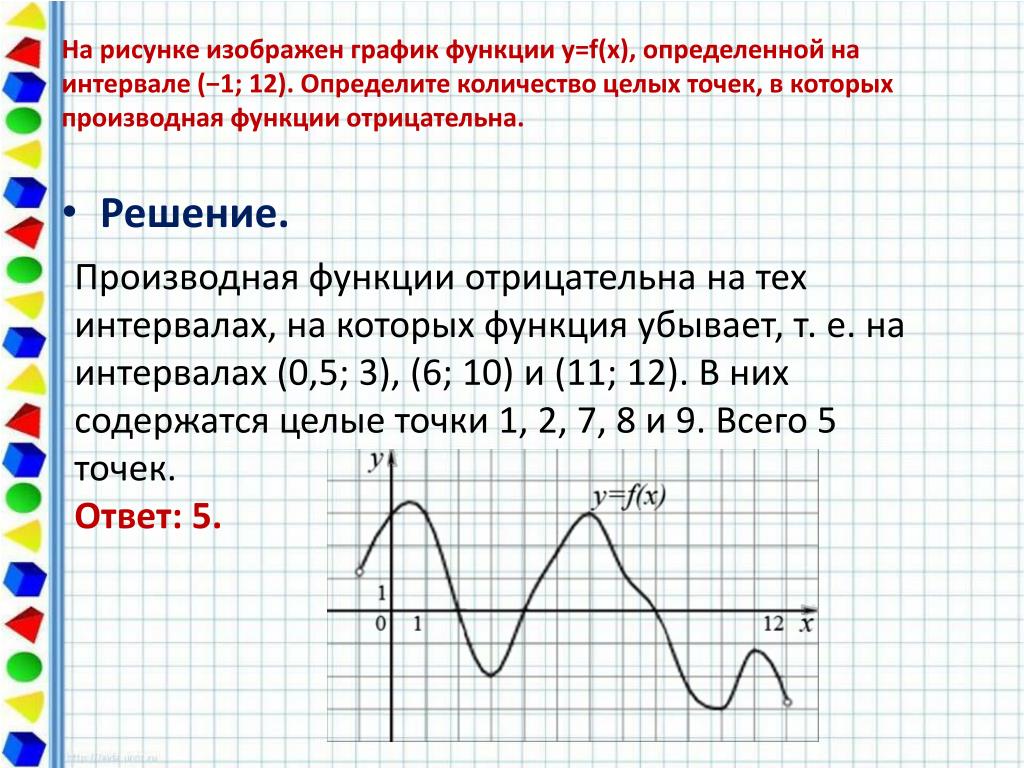
Обратите внимание на точки экстремума: точки максимума и минимума функции часто являются ключевыми для анализа ее поведения.

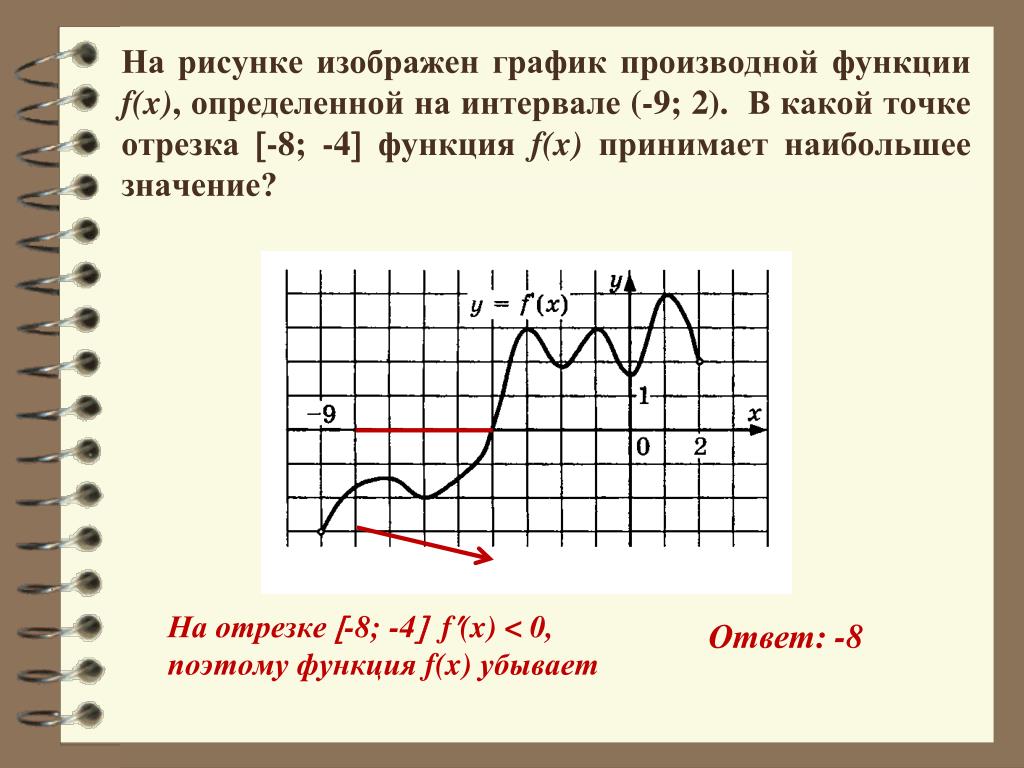
Учите правила дифференцирования: понимание и запоминание основных правил дифференцирования существенно облегчит процесс нахождения производных.

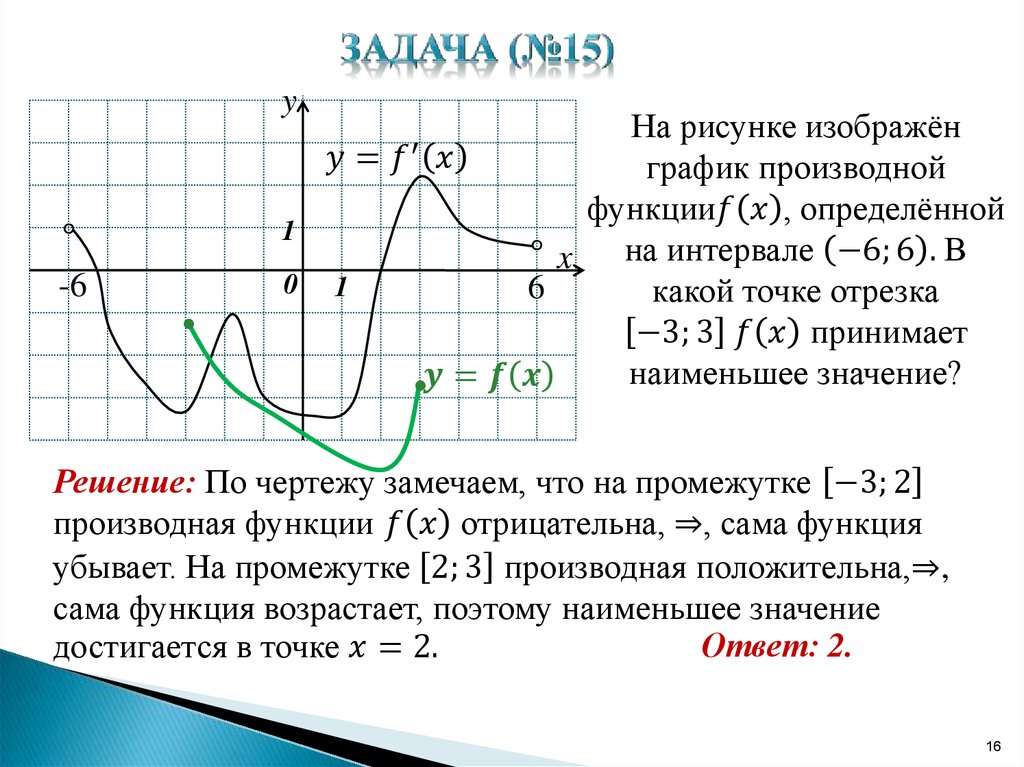
Применяйте производные на практике: анализ кривых, оптимизация и многие другие задачи требуют знания производных.

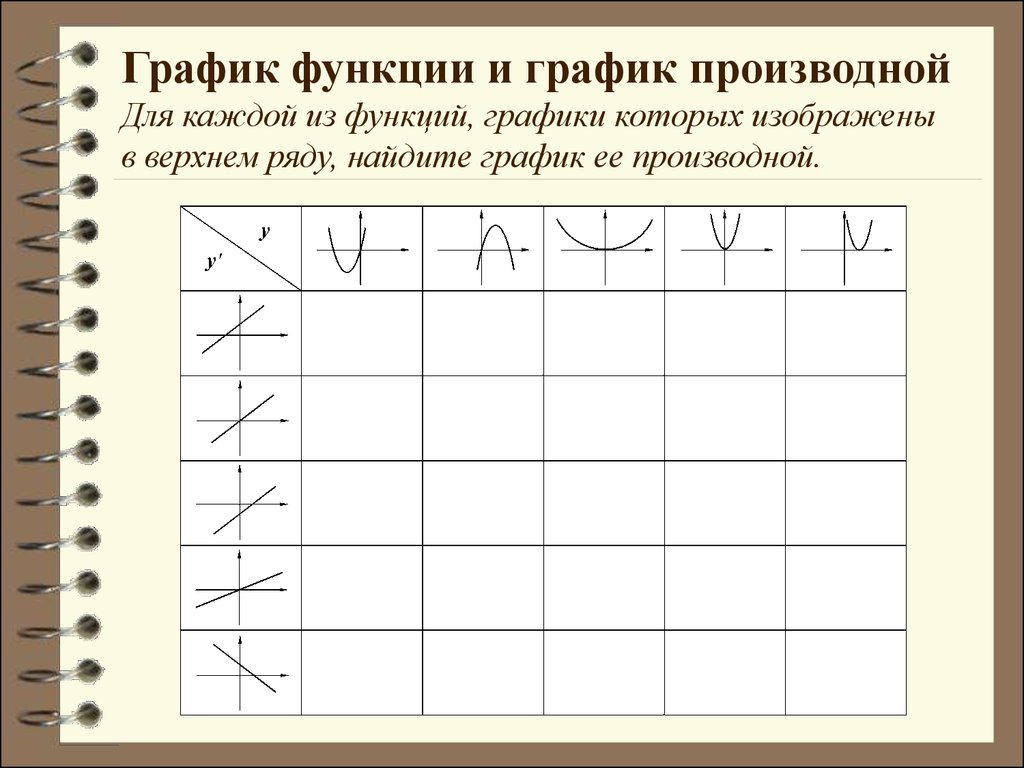
Ищите симметрии и другие особенности графиков: это поможет в быстром анализе функции и ее производной.

Пользуйтесь программными инструментами: такие программы, как GeoGebra и Desmos, могут существенно облегчить процесс обучения.

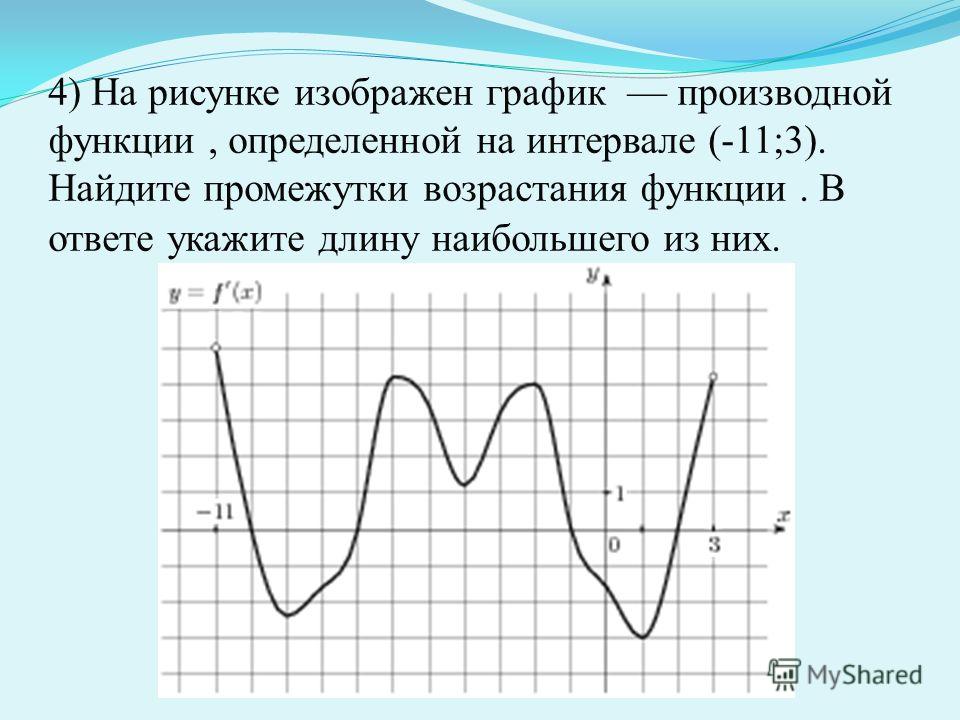
Разбирайте примеры из учебников и задачников: они содержат множество полезных примеров и упражнений для практики.

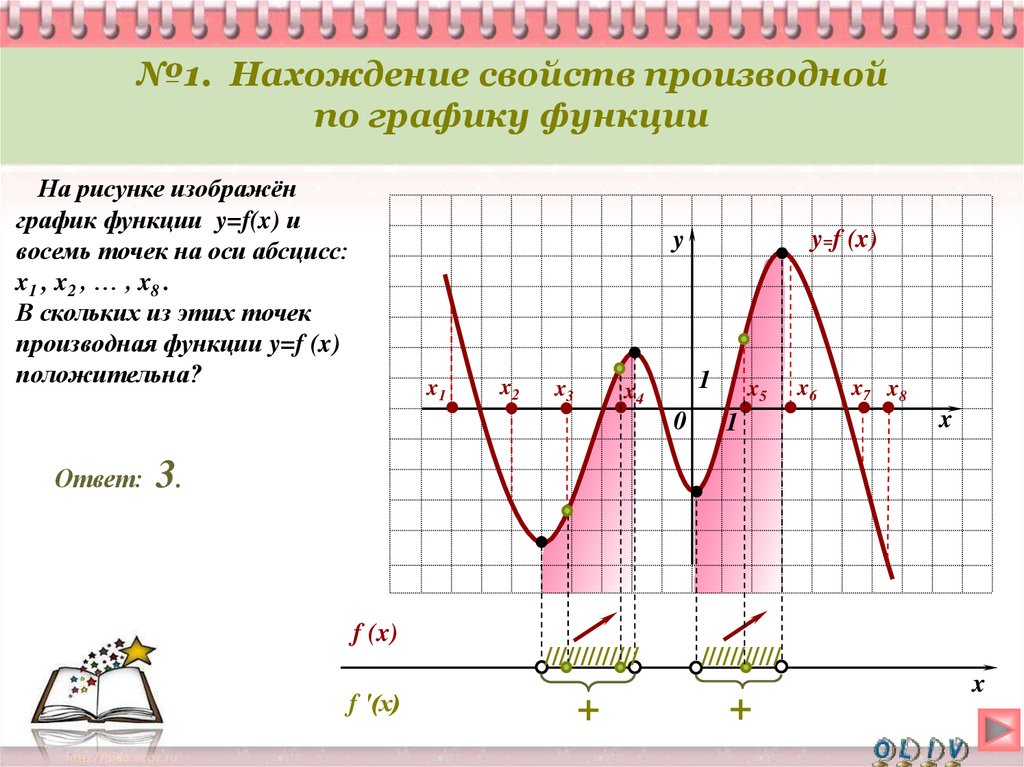
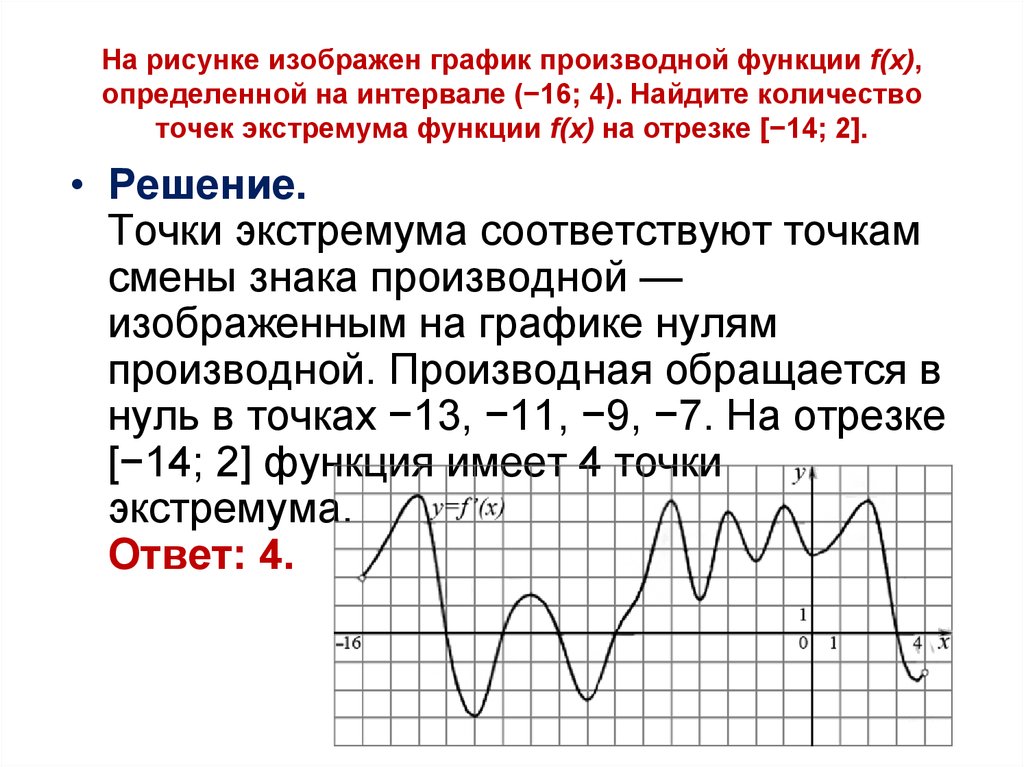
Не забывайте о физическом смысле производной: это скорость изменения величины, что полезно в разных прикладных задачах.