Основы уравнений кривых: советы по построению и интерпретации
В этом разделе вы найдете полезную информацию и советы по уравнениям кривых, включая методы построения графиков, их анализ и практические примеры. Уравнения кривых играют важную роль в математике и могут применяться в различных областях, таких как физика и инженерия. Узнайте, как правильно интерпретировать графики и решать задачи, связанные с кривыми.


Для начала изучите основные виды кривых, такие как окружности, эллипсы, параболы и гиперболы. Это поможет вам лучше понять, как различные уравнения влияют на графики.
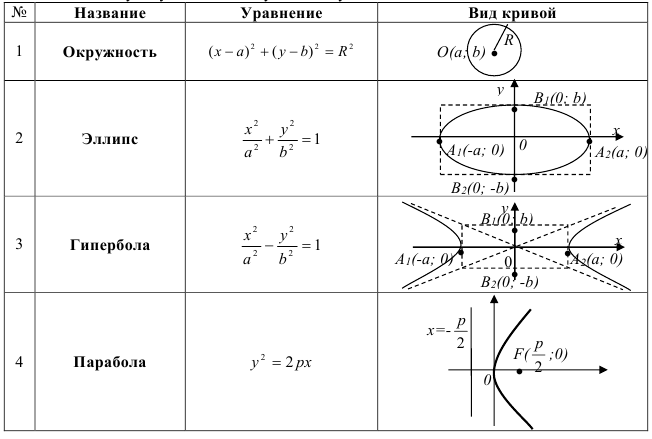
Используйте графические калькуляторы или программное обеспечение для построения кривых. Это облегчит процесс и даст наглядное представление о форме графика.
Приведение кривой второго порядка к каноническому виду. Пример


Понимание свойств кривых, таких как фокусные точки и асимптоты, может существенно помочь в анализе графиков и решении задач.

Работая с уравнениями, обязательно обращайте внимание на коэффициенты и их влияние на форму графика. Малейшие изменения могут существенно изменить вид кривой.
Регулярно практикуйтесь в решении различных задач по уравнениям кривых. Чем больше практики, тем легче будет воспринимать и анализировать новые уравнения.
Математика без Ху%!ни. Кривые второго порядка. Эллипс.
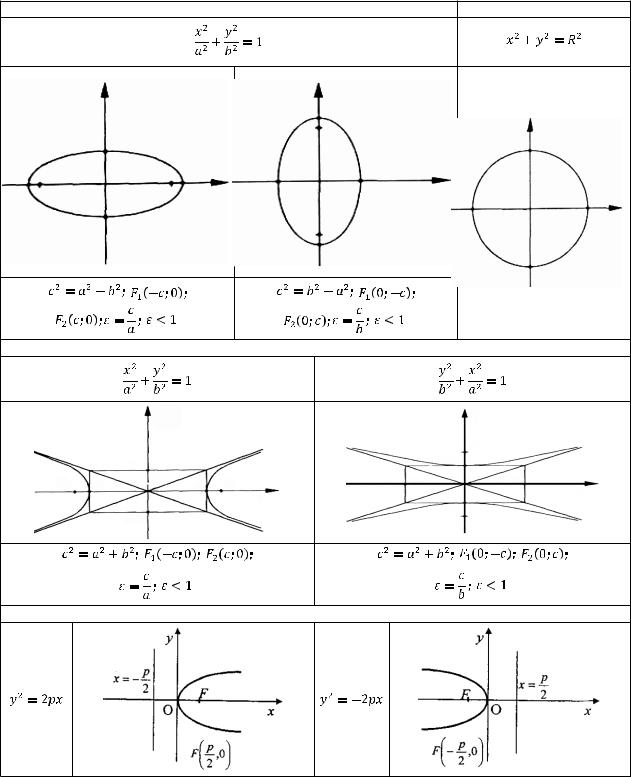
При решении задач старайтесь использовать различные методы проверки, чтобы убедиться в правильности построенного графика.

Читайте дополнительные ресурсы и статьи, чтобы углубить свои знания и понять более сложные аспекты уравнений кривых.
Работайте над улучшением своих навыков интерпретации графиков, чтобы быстрее и точнее находить решения задач.

При изучении уравнений кривых полезно использовать визуальные пособия, такие как графики и диаграммы, для лучшего понимания материала.
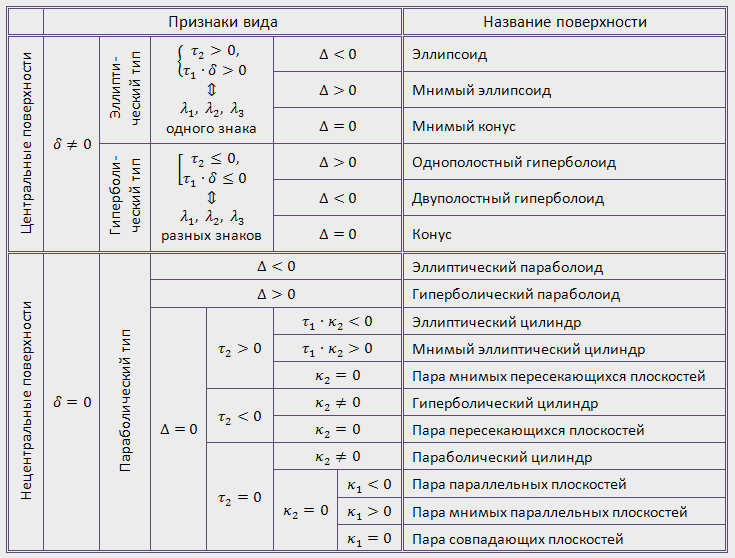
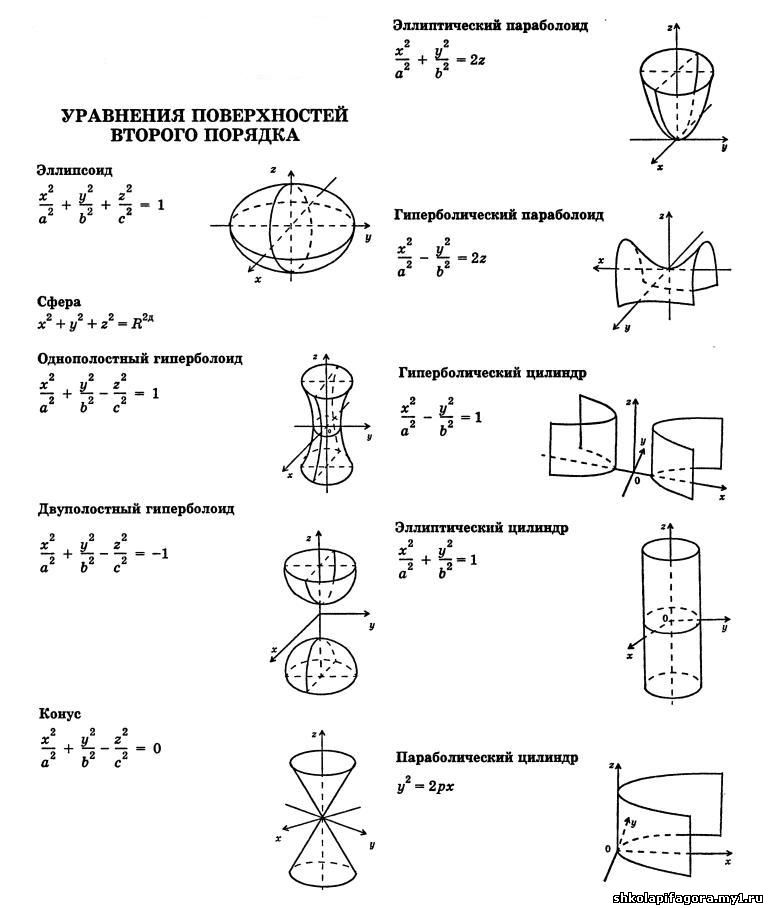
Уравнения кривых в пространстве


Обсуждайте решения задач с другими студентами или преподавателями, чтобы получить различные точки зрения и улучшить свои навыки.