Понимание остова графов: ключевые аспекты и советы
Остов графа – это подграф, который соединяет все вершины графа минимальным числом рёбер. В этой статье мы рассмотрим, как найти остов графа и приведём полезные советы по данной теме.

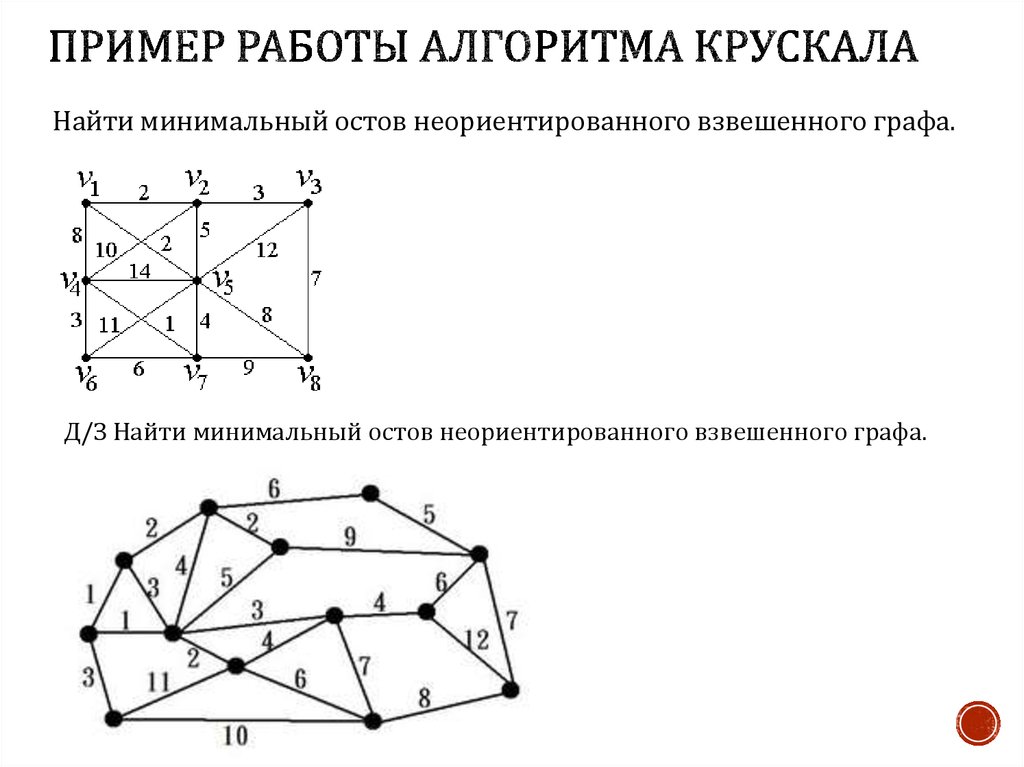
Начните с определения всех вершин графа и списка рёбер, соединяющих эти вершины.
Графы 1. Основные понятия

Используйте алгоритм Крускала или Прима для нахождения минимального остова графа.
4.9 Ациклические графы. Остовы. Алгоритмы Краскала, Прима.
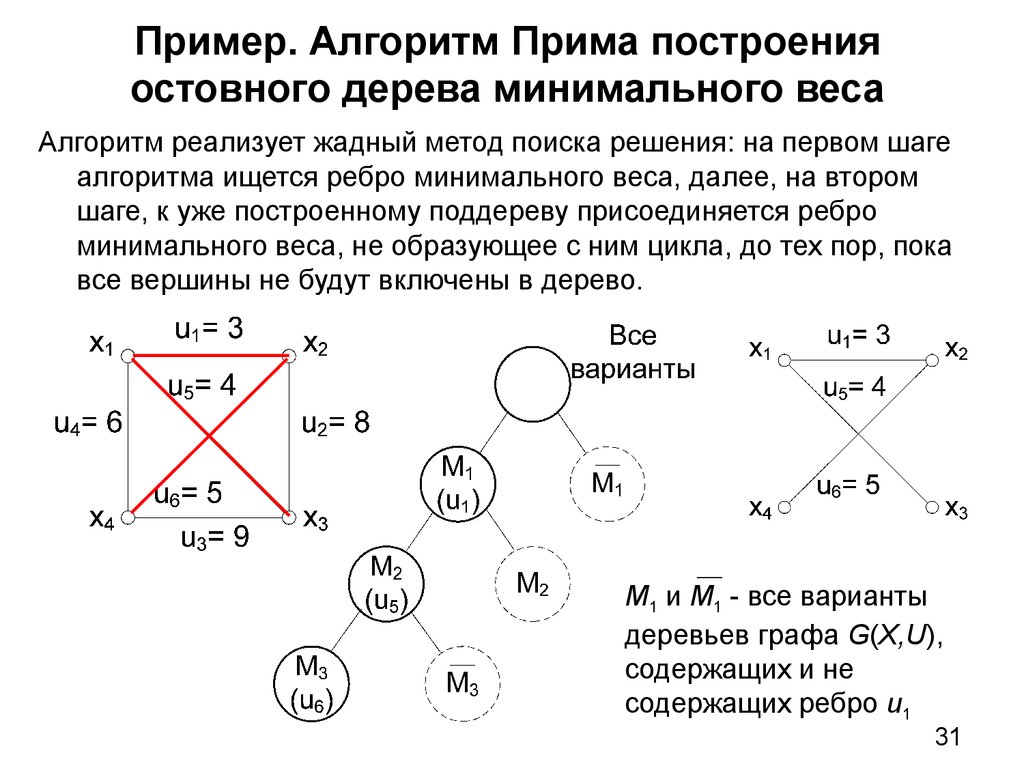
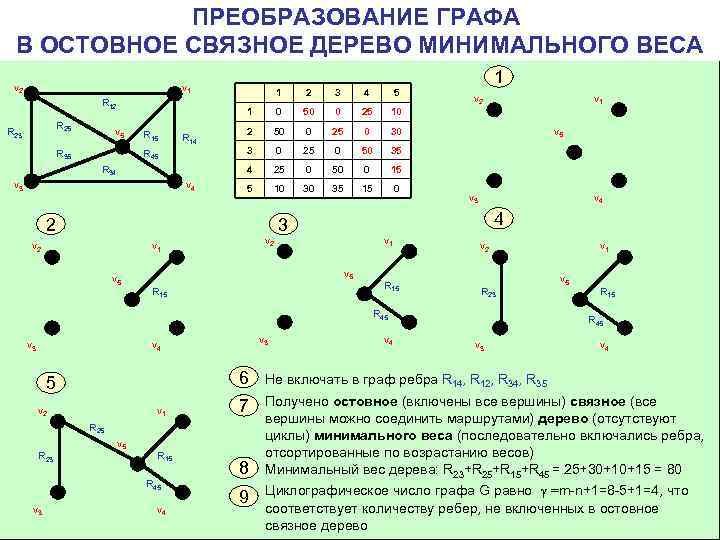
Проверяйте, чтобы остов не содержал циклов, иначе это нарушит его определение.
КАК РАБОТАЮТ ГРАФЫ - СТРУКТУРЫ ДАННЫХ

Обратите внимание на вес рёбер при выборе рёбер для остова – минимизируйте общую сумму весов.
Минимальное остовное дерево графа
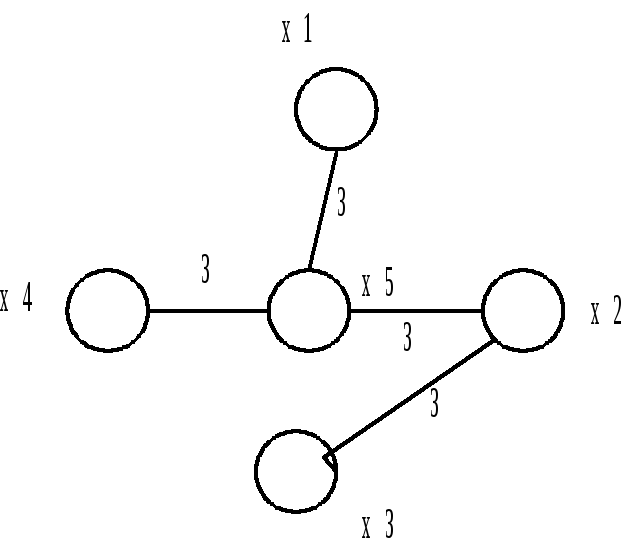
При использовании алгоритма Крускала сначала отсортируйте все рёбра по возрастанию веса.
Выживание на плоту Быстрый старт // Survival on Raft


В алгоритме Прима начните с произвольной вершины и постепенно добавляйте рёбра, соединяющие уже включённые вершины с новыми.
Построение остова может быть полезно для оптимизации сетевых маршрутов и снижения затрат на прокладку кабелей.
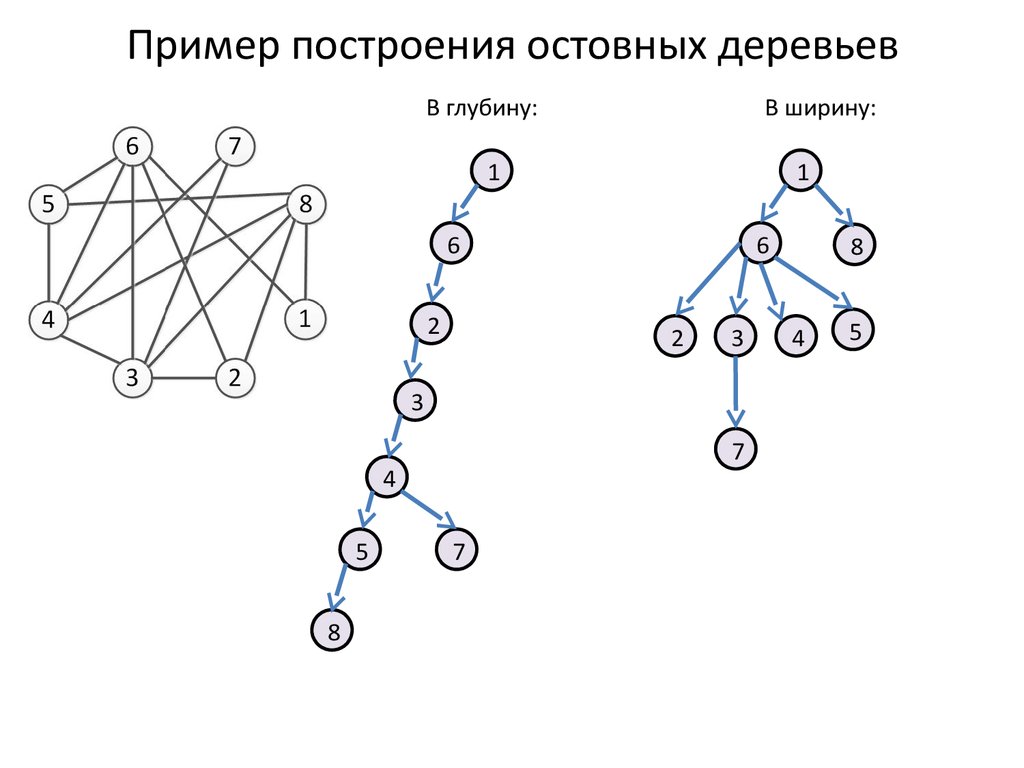
Изучите примеры и задачи на остов графа, чтобы лучше понять практическое применение алгоритмов.

Используйте специализированное программное обеспечение для автоматического построения остовов в сложных графах.

Не забывайте проверять корректность построенного остова, чтобы убедиться в его минимальности и связности.