Методы и советы по расчету площади криволинейного сектора

На этой странице вы найдете подборку фотографий и полезных советов, которые помогут вам понять и вычислить площадь криволинейного сектора. Это руководство включает в себя шаги, формулы и примеры, которые сделают процесс расчета более понятным и доступным.

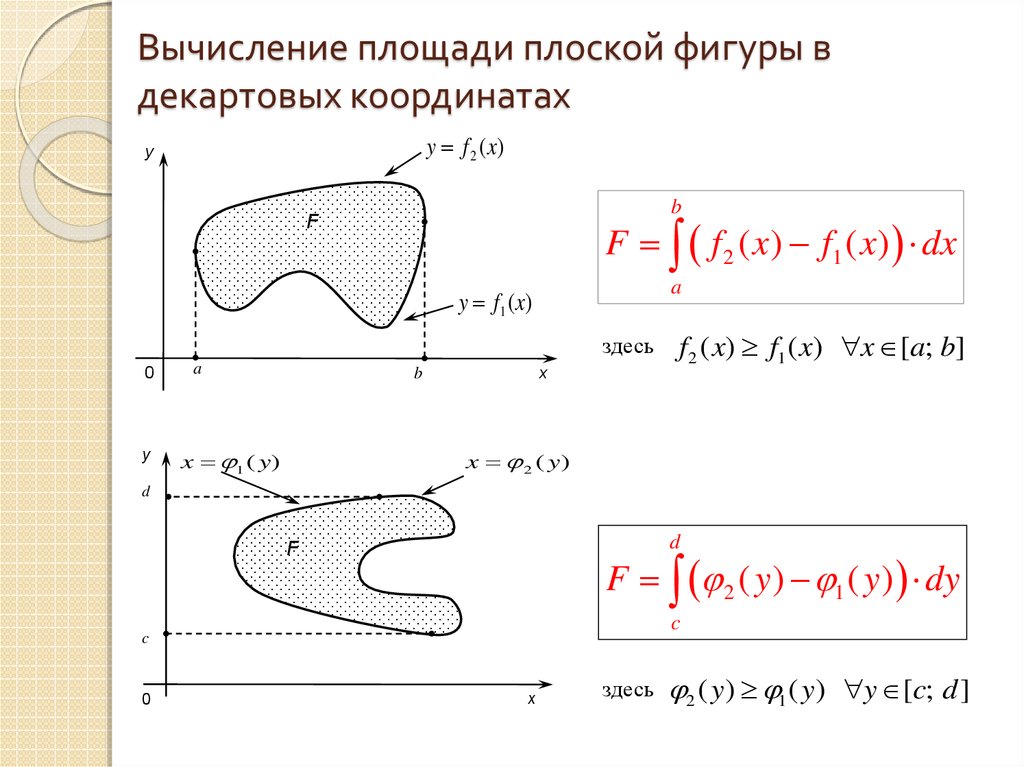
Используйте точные инструменты для измерения дуги и радиуса, чтобы избежать ошибок в расчетах.

Запомните формулу площади сектора: A=12R2θA = /frac{1}{2} R^2 /thetaA=21​R2θ, где RRR — радиус, а θ/thetaθ — угол в радианах.

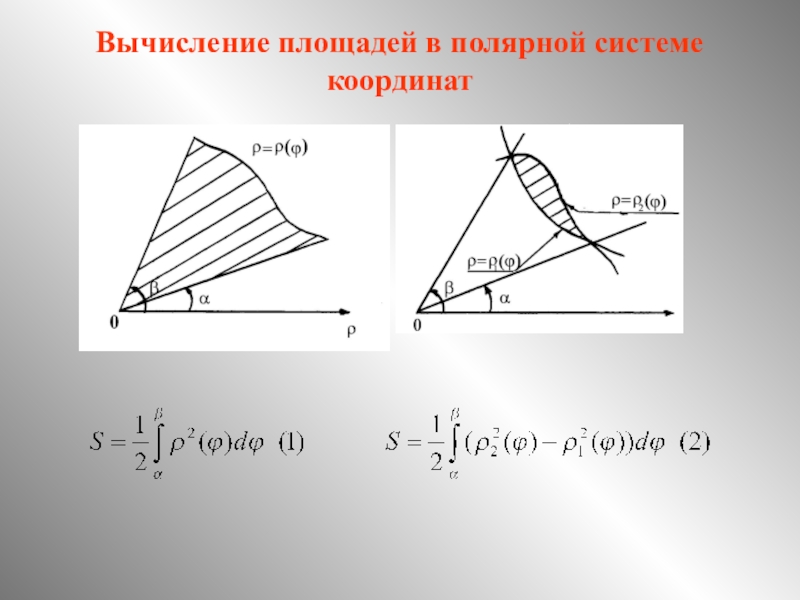
Убедитесь, что угол θ/thetaθ измеряется в радианах, а не в градусах. Для перевода градусов в радианы используйте формулу: θрад=θград⋅π180/theta_{/text{рад}} = /theta_{/text{град}} /cdot /frac{/pi}{180}θрад​=θград​⋅180π​.

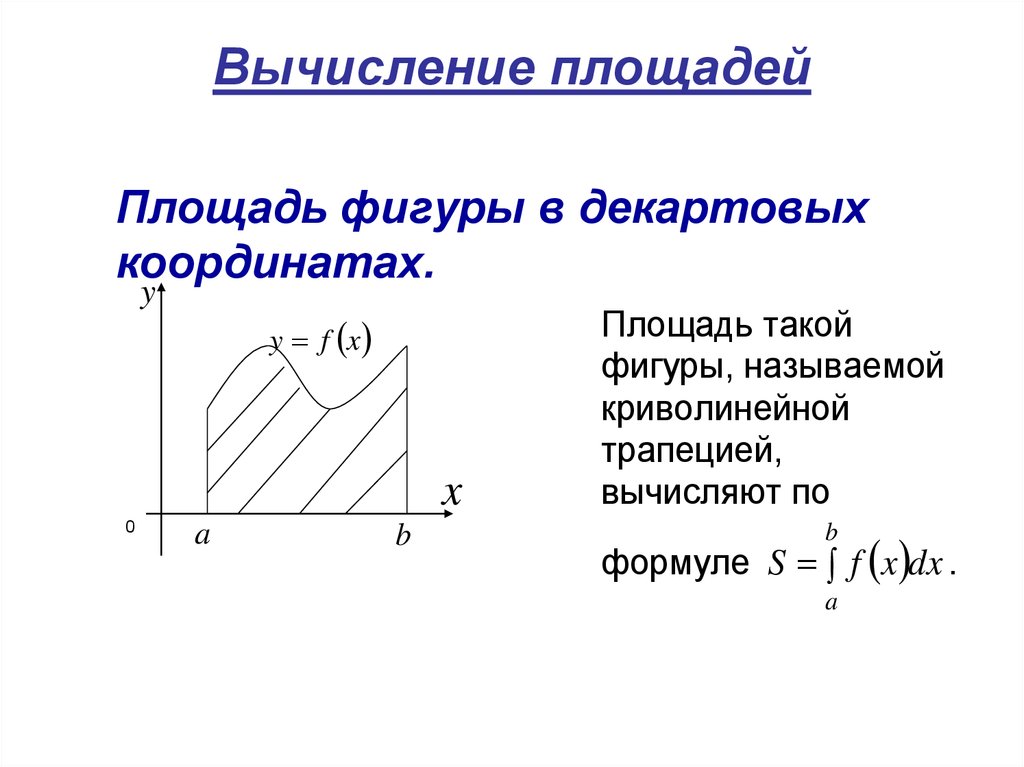
Если сектор является частью круга, определите его полный радиус для более точного расчета площади.

Практикуйтесь на простых примерах перед тем, как переходить к более сложным задачам.

Используйте графические программы или приложения для визуализации криволинейных секторов и проверки своих расчетов.

При работе с большими углами разбивайте сектор на несколько частей для более точного расчета.

Обратите внимание на единицы измерения и всегда переводите их в одну систему перед началом расчетов.

Для более сложных фигур используйте интегралы для вычисления площади криволинейных секторов.

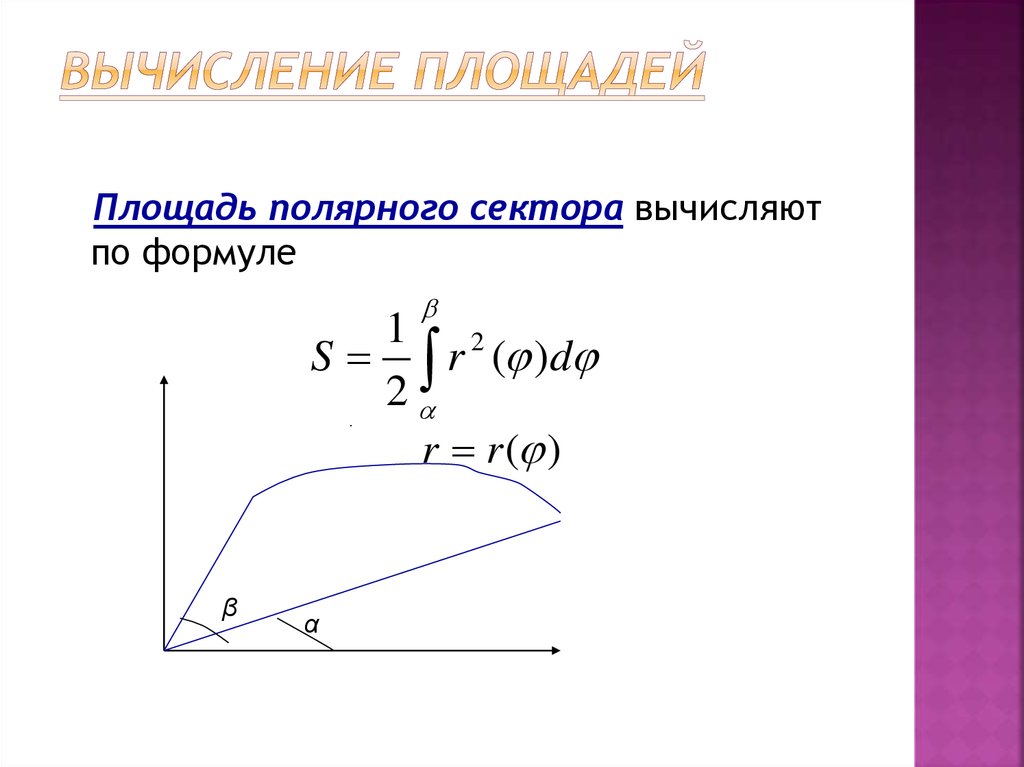
Старайтесь регулярно проверять и пересчитывать свои результаты для минимизации ошибок.